混合戦略の期待利得と最適反応の「極端な性質」を一般のp,qで理解する
【図斎 大】
期待利得をどのように計算するのかというのを本文ではキーパーとキッカーそれぞれの混合戦略を\(p=0.2, q=0.4\) と特定の数値例で説明しました。これを数値を特定せずに \(p,q\) という文字のままで,公式のように見せるのが,この文書の前半です。これは「混合戦略での最適反応の極端な性質」を数学的にきちんと理解することにつながります。本文では直観的に説明しましたが,この文書の後半では期待利得を \(p,q\) の式として表したのを活用して,ちょっと数学的に「極端な性質」がなぜ成り立つのかを説明します。
1 PK戦での期待利得の計算の一般化
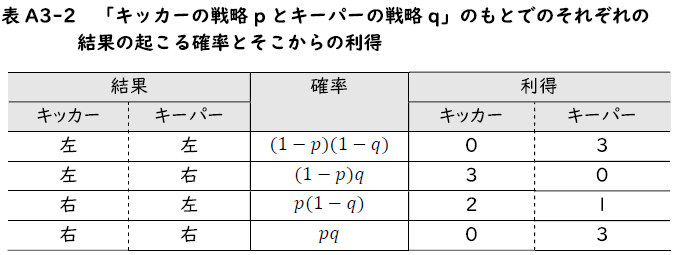
本文の2.3項ではキッカーが右サイドを攻める確率\(p\)を0.2, キーパーが右サイドを守る確率\(q\)を0.4として期待利得を求め,そして表3-4では\( p,q\) を0.2刻みで利得表を示しました。ここではモデル3.1のPK戦の利得表(表3-1)を引き続き考えつつ,期待利得の計算を一般化しましょう。つまり\( p,q\) に数字を代入せず,このままで期待利得を求めていきます。「キッカーが右をとる確率」が\(p\),そして[キーパーが右をとる確率]が\(q\)だったので,「両方がともに右をとる」という確率は\(pq\)となります。またキッカーが左をとる確率は\(1-p\)になるので,「キッカーが左を,キーパーが右をとる」という確率は\((1-p)q\)だとわかります。こうして戦略の組\((p,q)\)のもとでのそれぞれの結果の実現する確率分布は下の表A3-1のように求められます。
この計算を踏まえて,本文の表3-3のようにそれぞれの結果からの利得と確率をまとめたのが表A3-2です。
この表A3-2に基づいて,キッカーの期待利得を計算すると,
\[\begin{align}
&(1-p)(1-q)⋅0+(1-p)q⋅3 \\
&+p(1-q)⋅2+pq⋅0 \tag{A1} \\
\end{align}\]
と表されます。この式の\(p,q\)に任意の値,つまり任意のキッカー・キーパーの戦略を代入すれば,その戦略の組の下でのキッカーの利得が出てくるので,この式がキッカーの利得「関数」を表していると言えます。試しに式 (A1)の\(p,q\)に0.2と0.4をそれぞれ代入してみてください。すると,本文2.3項で求めた「キッカーの戦略0.2とキーパーの戦略0.4」からのキッカーの期待利得1.2が出てくるはずです。同様にキーパー(第2のプレーヤー)の利得関数も,以下の式のように計算されます。
\[\begin{align}
&(1-p)(1-q)⋅3+(1-p)q⋅0 \\
&+p(1-q)⋅1+pq⋅3 \tag{A2} \\
\end{align}\]
キッカーについては式(A1),キーパーについては式(A2)に,0.2刻み\(p,q\)を代入すると本文の表3-4を得ることができます。
2 最適反応の「極端な」性質の数学的な説明
モデル3.1におけるキッカーの最適反応を考えてみましょう。そこで,キーパーの戦略\(q\)を0.8としてみます。つまり,キーパーが左を選択する確率\(q\)が0.8となる混合戦略を選択しているとしましょう。一方で,キッカーが左を選択する確率を,ここでは\(p\)としたまま,変数で表現してみます。最適反応として知りたいことは,キーパーが戦略0.8を選択した場合に,キッカーの期待利得を最大にするような\(p\)の値を見つけることです。キッカーの期待利得を示す式(A1)に,ここで想定しているキーパーの戦略\(q=0.8\)を代入すると,
\[\begin{align}
&(1-p) ⋅0.2⋅0+(1-p)⋅0.8⋅3 \\
&+p⋅0.2⋅2+p⋅0.8⋅0 \\
&=-2p+2.4 \tag{A3} \\
\end{align}\]
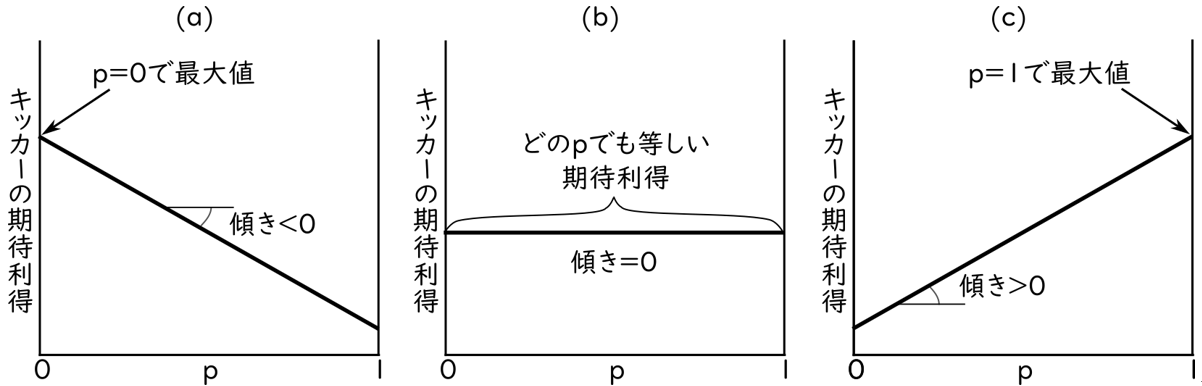
として求められます。傾きが負の1次式なので,このグラフは図A3-1 (a)のようになっているとわかります。右を選択する確率\(p\)の値が高くなるほど,この期待利得は小さくなることがわかります。したがって,できるだけ\(p\)を小さくしていくことがキッカーには好ましく,期待利得は,\(p=0\)で最大になっています。すなわち,キーパーの戦略\(q=0.8\)に対するキッカーの最適反応は\(p=0\)である,つまり左サイドに必ず蹴る純粋戦略だということがわかります。
同様に,\(q=0.6\)(右を確率0.6で選択)と\(q=0.2\)(右を確率0.2で選択)それぞれへのキッカーの最適反応を求めてみてください。それぞれを式(A1)に代入して,グラフを描いて,そこから期待利得を最大にするpを探せばよいわけです。\(q=0.8\)と同じく\(q=0.6\)に対してもグラフは図A3-1 (a)のようになり\(p=0\)が最適反応になったと思います。一方で,\(q=0.2\)に対しては,期待利得を示すグラフは図A3-1 (c)のようになり,右を選択する確率\(p\)の値が高くなるほど,期待利得が大きくなっていくことがわかります。よって,\(p=1\)が最適反応になります。
ただどちらにしてもキーパーの戦略を特定した後の,キッカーの期待利得をグラフにすると直線になります。それを確認するために式(A1)を
\[\begin{align}
&{-0(1-q)-3q+2(1-q)+0q}p+{ 0(1-q)+3q } \\
&=\bbox[#00EE00]{(2-5q) } p+\bbox[yellow]{3q} \\
\end{align}\]
と変形しましょう。ここで\(q\)はキーパーが決めているのでキッカーは変えられません。ですから,\(p\)のみがキッカーが動かせる変数であり,上式では■や■で囲ったところはキッカーにとっては動かせない数,すなわり「定数」になります。したがってこの期待利得の式は,キッカーにとっては\(\color{#00EE00}{■} p+\color{yellow}{■}\)という1次関数の式だと言えます。(例えば\(q=0.8\)を代入すると,\(\color{#00EE00}{■} =-2と\color{yellow}{■}=2.4\)という体数になり,この式\(\color{#00EE00}{■} p+\color{yellow}{■}\)は\(-2p +2.4\)となり(A3)と一致します。)なので,グラフにすると直線,特に ■が傾きで■が切片になります。そして,■ の中が負なら傾きが負でグラフは図A3-1(a)のようになり\(p=0\)で最大値, ■の中が正なら傾きが正でグラフは図A3-1 (c)のようになり\(p=1\)で最大値になるわけです。まとめると,傾きがゼロでない限りは,\(p=0\)か\(p=1\)という端,つまり純粋戦略で期待利得は最大になります。実際,この2つの端で期待利得が異なれば傾きはゼロではありません。このことから性質A)が導かれます。
\(q\)を0から1に連続的に増やしていくと■の中,つまり傾きが正から負に変わっていきますね。もちろんその途中で傾きがゼロになります。このときのキッカーの利得のグラフは図A3-1 (b)のようになり,どの\(p\)でも同じ期待利得になることが見てとれます。このときの\(q\)は ■の中をゼロとした式,つまり\(2-5q=0\)を解くことで\(q=0.4\)だとわかります。上の式変形で\({-0(1-q)-3q+2(1-q)+0q}\)が\(\bbox[#00EE00]{(2-5q)}\)になっていた,つまりこの2つは同じです。なので,\(2-5q=0\)というのは前者の方をゼロにしたもの,つまり
\[0(1-q)q+3q=2(1-q)+0q\]
とも書けますが,これは左辺が\(p=0\)からの,右辺が\(p=1\)からの期待利得を表しています。つまり,\(q=0.4\)は,この2つの純粋戦略からの期待利得が同じになることから導かれることから注意してください。これが性質B)の状況です。
以上の議論をまとめると,\(q=0.4\)に対しては,キッカーにとってどんな戦略\(p\)でも最適反応になり,その\(q\)を境目として,それよりも\(q\)が小さいと\(p=1\)が,\(q\)が大きいと\(p=0\)が最適反応になり,本文で示した結果になります。
ここまで \(q\)に具体的な数字を与えて性質A),B)を導きましたが,この議論の肝は,\(q\)を定数として与えると利得関数が\(p\)の1次関数になること,そしてその傾きの中がまた\(q\)の1次関数になっていることです。そしてそれぞれの変数に関して1次関数になっているのは,偶々ではなく,利得表(本文の表3-1)のような事後の結果の利得と表A3-1のような2者の混合戦略での確率の積を掛け合わせて期待利得を求めること自体から来ています。したがって,性質A),B)は違うゲームでも成立する一般的な性質なのです。