通貨危機

PDFファイル

【浅古泰史】

ゲーム理論の応用先は幅広く，マクロ経済学に関わるトピックにも応用がされています。ここでは，マクロ経済学的トピックへの応用例として，通貨危機を考えてみましょう。

まず，通貨危機が生じるメカニズムを，簡単に説明していきます。貨幣の価値は，さまざまな要因で変わっていきます。ものすごく単純に言ってしまえば，その国の経済力が高まれば通貨価値は高まりますし，弱まれば低まります。1ドル100円が1ドル200円に変わるということは，円の価値が下がることになります。アメリカで売られている1ドルのリンゴを買うために，100円だけ支払えばよかった状態が，その倍の200円も支払う必要がある状態に変わったので，円の価値が下落したと考えるわけです。物の売買と同様に，多くの円が売りに出され，ドルなどの外貨と交換されていけば，市場に円が多く供給されることにより，その価値は下落します。逆に，円が買われれば，円の価値は高まります。このように為替レートが頻繁に変更されてしまうようならば，その国に投資をするリスクが高まっていきます。そのリスクを低減し，海外からの投資を呼び込むために，固定相場制を採用する国が，主に途上国を中心に多くありました。

固定相場制とは，為替レートを固定し続ける制度です。例えば，1ドル100円と決めたならば，どれだけ円やドルの価値が変わろうとも，この為替レートを維持し続ける制度です。ただし，「固定する」と宣言したところで，簡単に固定されるわけではありません。円の価値が下がってしまえば，為替市場では，1ドル100円ではなく，150円や200円で取引されてしまうわけです。そこで政府は「何があっても，政府が100円と1ドルを交換してあげよう」と言うわけです。例えば，円の価値が下がっていると思われている状態でも，100円で1ドルと交換できるならば，わざわざ200円で1ドルしか得られないような為替レートで円を売ってドルを買う人は出てきません。固定相場制が維持されているかぎり，円の価値は暴落しないわけです。しかし，そのためには政府は多額のドルを用意しておく必要があります。これを，外貨準備と言います。どんなに円が売られても，ちゃんと100円と1ドルを交換してあげるレートを維持するために，どんどんドルを拠出しないといけないため，固定相場の維持のためには，十分な額の外貨準備が必要です。しかし，もし政府の外貨準備がなくなり，そこで100円と1ドルの交換ができなくなればゲームオーバーです。もう固定相場は維持できず，変動相場に移行し，一気に円の価値は暴落していくことになります。このようにして引き起こされる通貨価値の下落を通貨危機と言います。国内の資産価値は暴落し，輸入品も急激に高くなるなど，実体経済にも大きな悪影響を与えてしまいます。

一方で，通貨危機によって，投資家は利益を得ることができるチャンスがあります。例えば，1万円を持っている投資家が，1ドル100円の為替レートのときに，100ドルを手に入れます。その後，通貨価値が暴落し，例えば1ドル500円になったときに，今度は100ドルを円に換えると5万円が手に入ります。一気に5倍になるわけです。このように。固定相場のときに円を大量に売り，変動相場に移行して通貨価値が下落した後にその通貨を買い戻すことによって大きな利益を得ることができます。よって，投資家の中には特定の国の通貨を大量に売ることによって，通貨危機を引き起こそうとする人たちが出てきます。このように市場に攻撃を仕掛けて利益を得る行為を，投機と言います。

1990年代は，このような通貨危機が固定相場制を採用していた国々を中心に多発した10年でした。92年から93年にかけて欧州で，94年から95年にかけてメキシコで，97年，98年，99年には，それぞれアジア，ロシア，ブラジルで通貨危機が起こりました。その中で，日本も大きな影響を受けたアジア通貨危機を取り上げてみましょう。

90年代に生じた各国の通貨危機で大きな役割を演じたのが，前述した投資家による投機活動でした。多くの通貨危機において，このような投機が突然，予期できないタイミングで大々的に生じることになります。しかし，投資家たちは綿密に話し合い計画を練ってから通貨売りを仕掛けたわけではありません。なぜ投資家たちは，足並みを揃えて急に攻撃を仕掛けることができたのでしょうか。

投資家たちが投機に走り自国通貨の売りをしている場合，その国の政府・中央銀行は固定相場を維持するために，前述した通り自国通貨を買い支えようとします。そのためには，十分な外貨準備が必要です。例えば，その国の財政赤字が大きく，自国通貨の発行によりその赤字を賄っている場合には，投資家が投機に走る以前に自国通貨の価値は減少してしまっています。その場合，固定相場制を維持するために政府は外貨を売らなければなりません。よって，経済・財政基盤が弱く，財政赤字を多く抱える国の外貨準備高は少なくなり，投資家たちの投機により通貨危機が引き起こされやすくなります。しかし実際には，経済・財政基盤がそれほど弱くない国でも通貨危機は生じました。その理由を，以下のモデルを使って考えてみましょう。

ここで単純化のために，政府・中央銀行は，できるかぎり通貨価値の維持を試みるだけと考え，プレーヤーとしては分析しません。また，本来は多くの投資家がいるべきですが，これも単純に2人の投資家のみを考えましょう。

【モデル(通貨危機)】
2人の投資家がいる。ある国に対して，通貨危機を引き起こすための投機を行う(「投機」)か否か(「否」)を決定する。その国の外貨準備高は少ないわけではなく，投機を1人だけが仕掛けてきた場合には耐えることができる。しかし，2人に仕掛けられると耐えられずに，通貨価値は暴落することになる。投資家は何も仕掛けなかった場合には，利益を得られず利得は0となる。2人とも投機を仕掛けた場合には，通貨価値が暴落することで稼ぐことができるため，10の利得を得る。もし，自分だけが投機を仕掛けた場合，通貨価値は暴落せず，損失を被るため利得は-2になる。

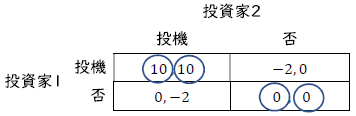
利得表を用いて，このモデルを表すと，上の表になります。相手が「投機」を選んでいる場合は，「投機」が最適応答です。また，相手が「否」を選んでいる場合は，「否」が最適応答です。よって通貨危機ゲームでは，2人とも「投機」を選んでいる(投機，投機)と，2人とも「否」を選んでいる(否，否)の2つがナッシュ均衡です。このゲームにはもう1つ，混合戦略を用いた均衡も存在しますが，ここでは議論しません。興味があれば，第3章を読んだ後に計算してみてください。

通貨危機ゲームには2つのナッシュ均衡が存在しています。この2つの中で，(投機，投機)のナッシュ均衡はパレート最適です。一方で，もう1つのナッシュ均衡である(否，否)も含め，他の3つの戦略の組み合わせは，パレート最適ではありません。全て，(投機，投機)に変更することで，2人とも利得を10まで高めることができるからです。よって，このゲームは鹿狩りゲームと同じ利得構造になっています。ただし，このパレート最適な均衡では通貨危機が発生し，投資家以外の多くの人々は大きな経済的損失を被ります。あくまで，投資家2人にとってパレート最適なだけで，社会全体にとって最適なわけではありません。

通貨危機は，経済状態がそれほど悪くなかったとしても，突然予期できないタイミングで，多くの投資家が一気に投機を仕掛けることで生じてしまうことがあります(Rose and Svensson, 1994など)。そこには投資家の期待が大きな影響を与えるとも言われています。投資家たちが弱気なときには何も起こらないものの，投資家たちが強気になり，他の投資家も一緒に投機攻勢をかけてくるはずだと信じて行動をした場合，その予想が事後的に実現することとなり，通貨危機が生じるというものです(Obstfeld, 1996など)。この議論は本書の定義2.4で示した，事後実現的な予想と関わります。通貨危機が生じない(否，否)という均衡では，投資家は他の投資家が投機をしないと予想しているため投機をしません。つまり，投資家たちは「弱気」になっています。そして，皆が弱気なときには投機は生じないため，「相手は投機しない」という予想は事後的に実現してしまうわけです。一方で，通貨危機が生じる(投機，投機)という均衡では，投資家は相手も投機をしてくると信じることで「強気」になり，投機を仕掛けます。よって，「相手は投機する」という予想が事後的に実現するわけです。

ここで紹介したモデルは，通貨危機の第2世代モデル(Obstfeld, 1996など)や第3世代モデル(Chang and Velasco, 2001など)と言われているものを単純化したものです。通貨危機が生じる経済財政状況を明らかにした第1世代モデル(Krugman, 1979など)に続き，通貨危機が生じる均衡と生じない均衡の複数均衡が存在している状況を第2・3世代モデルでは分析しています。その第2・第3世代モデルに対しては，「複数ある均衡のうち，なぜ通貨危機が発生する均衡が生じると投資家は信じるようになるのかを説明できていない」という批判がありました。その問題を解決するモデルの提示も，その後行われています。本書は，国際金融の専門書ではないため詳細は省きますが，より知りたい読者は竹田(2007)を参照してください。

練習問題(通貨危機ゲームの拡張)
本稿の通貨危機のモデル分析では，外貨準備高が極端に不足しているわけでも，また極めて潤沢にあるわけでもない国を分析対象とした。一方で投資家が抱く期待にかかわらず，外貨準備高が極端に不足している場合には通貨危機が生じ，外貨準備高が潤沢にある場合には通貨危機は生じないことも指摘されている。この指摘を確認するために，以下の小問に答えよ。

1. 外貨準備高が極端に不足している国を考えよう。1人の投資家が投機を仕掛けただけで，通貨価値は下落してしまうとする。利得表を書き直し，この場合のナッシュ均衡を示せ。
2. 外貨準備高が潤沢にある国を考えよう。2人の投資家が投機を仕掛けたとしても，通貨価値は下落しないとする。利得表を書き直し，この場合のナッシュ均衡を示せ。

参考文献

• 竹田憲史(2007)「通貨・金融危機の発生メカニズムと伝染:グローバル・ゲームによる分析」『金融研究』26巻2号，pp.87-130.
• Chang, R., and A. Velasco (2001) “A Model of Financial Crises in Emerging Markets,” The Quarterly Journal of Economics, 116(2), pp. 489-517.
• Krugman, P. (1979) “A Model of Balance-of-Payment Crisis,” Journal of Money, Credit and Banking, 11(3), pp. 311-325.
• Obstfeld, M. (1996) “Models of Currency Crises with Self-Fulfilling Features,” European Economic Review Papers and Proceedings, 40 (3-5), pp. 1037-1047.
• Rose, A., and Svensson, L. (1994) “European exchange rate credibility before the fall,” European Economic Review, 38, pp. 1185–1216.