プレーヤーが3人の場合の利得表を用いた解法
【浅古泰史】
本書の第2章5節では,N人のゲームとして3人以上のプレーヤーがいる場合の分析方法を紹介しました。そこでは,利得表を使わずにナッシュ均衡を求めていました。3人以上の場合のゲームでは,無理に利得表を用いないことをお勧めしますが,プレーヤーの数がちょうど3人であり,かつ戦略の数が少ない場合には,利得表を用いた分析も可能です。このオンライン・コンテンツでは,利得表を用いて,3人のゲームにおけるナッシュ均衡を求める方法を紹介します。
プレーヤーが3人おり,その各プレーヤーはそれぞれ2つの戦略を有する場合を考えましょう。利得表に示すと,表1のようになります。利得表が2つありますね。それぞれの利得表は,プレーヤーが2人(プレーヤー1と2)だったときと変わりありません。縦に並んだ戦略TとDはプレーヤー1の戦略であり,横に並んだ戦略LとRはプレーヤー2の戦略になります。ここの部分は,2人のプレーヤーのゲームと一緒です。一方で,2つの利得表の上に,それぞれAとBという名前がついています。このAとBがプレーヤー3の戦略です。つまり,プレーヤー3は,左側の利得表を選ぶか,あるいは右側の利得表を選ぶかを決めるプレーヤーであるということになります。各マスに3つの数字が並んでいますが,最初から順番にプレーヤー1,プレーヤー2,プレーヤー3の利得です。例えば,左側の利得表の左上のマスは,プレーヤー1がTを,プレーヤー2がLを,そしてプレーヤー3がAを選んでいる状況下での利得を示しています。右側の利得表の左下のマスで各プレーヤーが選択している戦略は(D,L,B)ということですね。
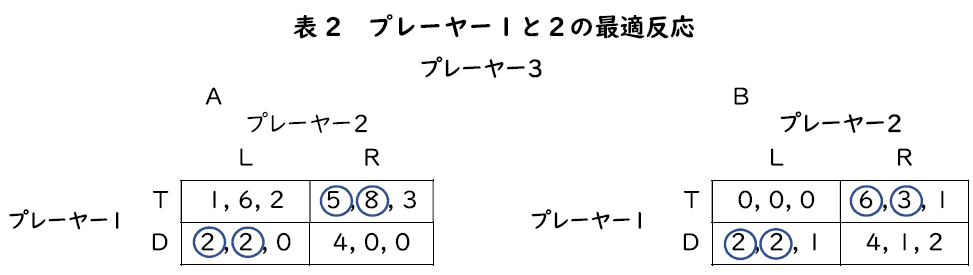
それではナッシュ均衡を求めていきましょう。まずは,最適反応を見つけていかなければなりません。プレーヤー1とプレーヤー2の最適反応を求める方法は,今までと変わりありません。プレーヤー1の最適反応から考えていきましょう。表2を見てください。3人のプレーヤーがいるので,プレーヤー2とプレーヤー3の2人の戦略の組に対する最適反応を考えないといけません。まず,プレーヤー2がLを選び,プレーヤー3がAを選んでいるとき,つまり(L,A)に対する最適反応は何でしょうか。この場合,左側の利得表の左側の列を見る必要があります。プレーヤー1がTを選べば1の利得ですが,Dを選べば利得は2になるので,(L,A)に対する最適反応はDです。なので,表2に〇をつけましょう。次に,プレーヤー2がRを選び,プレーヤー3がBを選んでいるときの最適反応を考えましょう。これは,右側の利得表の右側の列ですね。今度は,6>4からTが最適反応です。これを続けていくと,(R,A)に対する最適反応はTであり,(L,B)に対する最適反応はDだとわかります。
では,プレーヤー2の最適反応はどうでしょうか。まず,プレーヤー1がTを選び,プレーヤー3がAを選んでいるときの最適反応は,左側の利得表の上の行を見る必要があります。プレーヤー2がLを選べば6の利得ですが,Rを選べば利得は8になるので,(T,A)に対する最適反応はRです。〇をつけましょうね。次に,プレーヤー1がDを選び,プレーヤー3がBを選んでいるときの最適反応は,右側の利得表の下の行を見ます。今度は,2>1からLが最適反応ですね。これを続けていくと,(D,A)に対する最適反応はLであり,(T,B)に対する最適反応はRだとわかります。
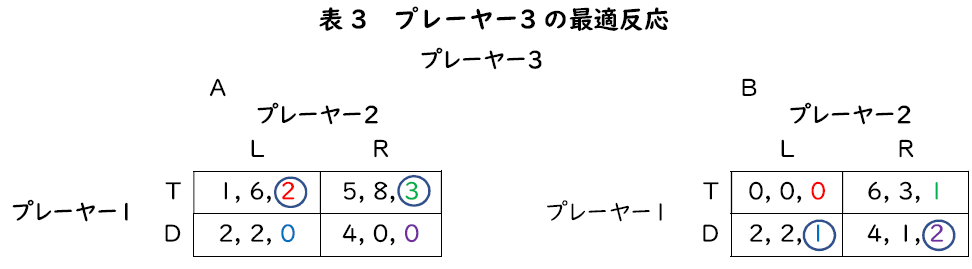
最後に,プレーヤー3の最適反応を探しましょう。表3を見てください。まず,プレーヤー1がTを選び,プレーヤー2がLを選んでいるときの最適反応を考えます。このとき,プレーヤー3がAを選べば,結果は左側の利得表の左上のマスになります。一方で,Bを選べば右側の利得表の左上のマスが結果です。この2つのマスにおけるプレーヤー3の利得は,赤色にしています。プレーヤー1がTを選び,プレーヤー2がLを選んでいるときに,プレーヤー3がA(左側の利得票)を選べば2の利得ですが,B(右側の利得表)を選べば利得は0になるので,(T,L)に対する最適反応はAです。表3のプレーヤー3の利得の部分に〇をつけましょう。次に,プレーヤー1がTを選び,プレーヤー2がRを選んでいる場合,Aを選べば左側の利得表の右上が,Bを選べば右側の利得表の右上が結果になります。ここでのプレーヤー3の利得は緑色にしています。この緑色の利得2つを比較するわけです。3>1ですから,(T,R)に対する最適反応もAです。このように他の場合も分析していきます。プレーヤー1がDを選び,プレーヤー2がLを選んでいるときは,2つの利得表の左下を(青色の利得)比較します。(D,L)に対する最適反応はBですね(0<1)。同様に,プレーヤー1がDを選び,プレーヤー2がRを選んでいるときも(2つの利得表の右下の紫色の利得の比較),最適反応はBです(0<2)。
これで全員の最適反応がわかりました。表2と表3を合わせて,全員が最適反応を選択している戦略の組は,(T,R,A)と(D,L,B)だとわかります。この2つがナッシュ均衡です。
ここでは2つの戦略を有する3人のプレーヤーがいるゲームを考えました。戦略の数が増えて,1人のプレーヤーが5つの戦略を有するとしましょう。この場合,利得表が5×5になるだけではなく,プレーヤー3も5つの戦略を持つわけですから,利得表の数も5つになります。また,戦略の数が2つでも,プレーヤーの数が4人になれば,表1をもう1つ書き,利得表の数を4つにしないといけません。戦略の数やプレーヤーの数が少し増えるだけで,書かなければいけない利得表の数はドンドン増えていくわけです。分析がややこしくなりそうですね。ですので,3人以上のゲームでは,本著の中で分析したように,しっかりと場合分けをしたうえで,利得表を用いずに分析していく方が無難だと思います。