【小俵将之・浅古泰史・森谷文利・図斎大】
問題7.1(ベイズ・ルール)
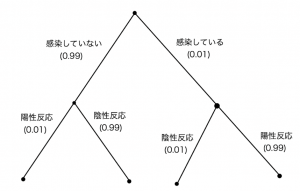
(ア)「ゲームの木」のように表現すると以下のようになる。
求めたい確率は
\[\textrm{Pr}(感染している|陽性)=\frac{\textrm{Pr}(感染している,陽性)}{\textrm{Pr}(陽性)} \]
である。ここで,周辺確率\(\textrm{Pr}(陽性)\)は次のように分解でき,
\[\begin{align}
&\textrm{Pr}(陽性)= \\
&\textrm{Pr}(陽性|感染している) \textrm{Pr}(感染している) \\
&+\textrm{Pr}(陽性|感染していない) \textrm{Pr}(感染していない)
\end{align}\]
同時確率\(\textrm{Pr}(感染している,陽性)\)は,この右辺の第一項である。つまり
\[\textrm{Pr}(感染している,陽性)=\textrm{Pr}(陽性|感染している) \textrm{Pr}(感染している).\]
よって,
\[\begin{align}
& \textrm{Pr}(感染している|陽性)= \\
&\scriptsize \frac{\textrm{Pr(陽性|感染している) Pr(感染している)}}{\textrm{Pr(陽性|感染している)Pr(感染している)+Pr(陽性|感染していない)Pr(感染していない)} } \\
&=\scriptsize \frac{(0.99) \cdot (0.01)}{(0.99) \cdot (0.01)+(0.01) \cdot (0.99) }= \frac{1}{2}
\end{align}\]
を得る。
答え:1/2
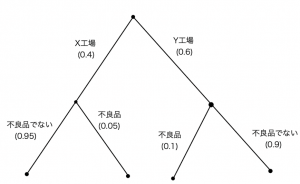
(イ)「ゲームの木」のように表現すると以下のようになる。
求めたい確率は
\[\textrm{Pr}(X工場|不良品)=\frac{\textrm{Pr}(X工場,不良品)}{\textrm{Pr}(不良品)} \]
である。ここで,周辺確率\(\textrm{Pr}(不良品)\)は次のように分解でき,
\[\begin{align}
& \textrm{Pr(不良品)}= \\
& \textrm{Pr(不良品|X工場)} \textrm{Pr(X工場)}+\textrm{Pr(不良品|Y工場)} \textrm{Pr(Y工場)}, \\
\end{align}\]
同時確率\(\textrm{Pr(X工場,不良品)}\)は,この右辺の第一項である。つまり,
\[\textrm{Pr(不良品,X工場)}=\textrm{Pr(不良品|X工場)} \textrm{Pr(X工場)}.\]
よって,
\[\begin{align}
& \textrm{Pr}(X工場|不良品)= \\
& \scriptsize \frac{ \textrm{Pr(不良品|X工場)Pr(X工場)} }{ \textrm{Pr(不良品|X工場)Pr(X工場)+Pr(不良品|Y工場)Pr(Y工場)} } \\
& \scriptsize = \frac{(0.05) \cdot (0.4)}{(0.05) \cdot (0.4)+(0.1) \cdot (0.6)}=\frac{1}{4} \\
\end{align}\]
を得る。
答え:1/4
問題7.2(迷惑メールモデルの一般化)
(ア)求めたい確率は
\[\begin{align}
& \textrm{Pr}(迷|有)=\frac{\textrm{Pr}(迷,有)}{\textrm{Pr}(有)} \\
& =\frac{ \textrm{Pr(有|迷)Pr(迷)} }{\textrm{Pr(有|迷) Pr(迷)+Pr(有|友)Pr(友)} } \\
& =\frac{(0.4)(0.5)}{(0.4)(0.5)+x(0.5) }
\end{align}\]
である。これに\(x=0.3\)を代入すれば,
\[\textrm{Pr}(迷|有)=\frac{4}{7}\]
を得る。
答え: 4/7
(イ) 今度は\(x=0.4\)を代入すれば
\[\textrm{Pr}(迷|有)=\frac{1}{2}\]
を得る。
答え:1/2
(ウ) 当選という言葉が入っているメールが迷惑メールである確率は,友人のメールに「当選」が含まれる確率xが上がると,下がる。これは,
\[\textrm{Pr}(迷|有)=\frac{(0.4)(0.5)}{(0.4)(0.5)+x(0.5)}\]
が\(x\)の減少関数であることからも分かる。
(解説)
(イ)\(x=0.4\)の場合,「当選」という言葉が含まれていようとなかろうと,迷惑メールの確率は事前と事後で変化していない(つまり,\(\textrm{Pr}(迷|有)=\textrm{Pr}(迷)\))となっていることに注意してください。このような場合には,語句が含まれているかどうかということは,なんら情報を与えていないことになります。このような状況を,独立であるといいます。もう少し一般的に考えましょう。事前確率と事後確率が一致している条件
\[\textrm{Pr}(迷|有)=\textrm{Pr}(迷)\]
に,条件付確率の定義\(\textrm{Pr}(迷|有)=\frac{\textrm{Pr(迷,有)}}{\textrm{Pr(有)}}\) を代入して変形すると,
\[\textrm{Pr}(迷,有)=\textrm{Pr}(迷) \textrm{Pr}(迷)\]
となります。すべての事象について上記の式が成立するとき,「迷惑メールの有無」と「語句の有無」は独立している(independent)と定義されます。高校の数学では,大小二つのさいころを振る状況を取り扱い,「大きいさいころの試行」と「小さいさいころの試行」は独立しているという話を学習しました。これは,「大きいさいころを振って結果をみても,小さいさいころの出目に関する情報が手に入らない」ということを想定していることになります。独立性とベイズ・ルールは密接な関係にあることを確認してください。
問題7.3(ベイジアン・ナッシュ均衡)
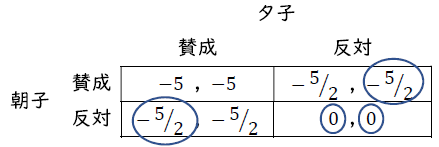
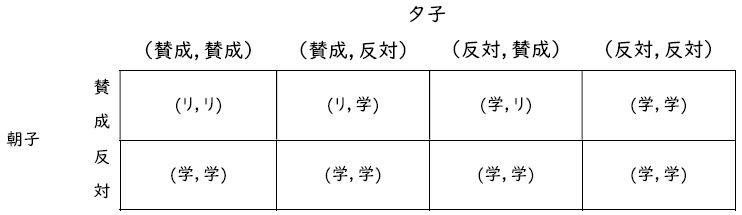
(ア)朝子も夕子も,アモーズが美味しいかどうかを知らないので行動を「美味しいか否か」に依存させることは出来ない。よって,利得表を作るためには(朝子の行動, 友子の行動)のそれぞれに対して期待利得を求めればよい。
①(反対, 反対)の場合:
両者の期待利得は
\[\underbrace{ \frac{4}{10} }_{ 美味しい確率 }×0+\underbrace{ \frac{6}{10} }_{ 美味しくない確率 }×0=0\]
である。
②(賛成, 賛成)の場合:
両者の期待利得は
\[ \frac{4}{10} \overbrace{ 10 }^{ 美味しいときのアモーズから利得 }+\frac{6}{10}× \overbrace{ -15 }^{ 美味しくない時のアモーズからの利得 }\]
である。
③(賛成, 反対)もしくは(反対, 賛成)の場合:
アモーズが美味しいか否かに関わらず,\(1/2\)の確率でアモーズに行き,\(1/2\)の確率で学食に行く。よって,両者の期待利得は
\[\frac{4}{10} \left\{ \frac{1}{2}×10+\frac{1}{2}×0 \right\}+\frac{6}{10} \left\{ \frac{1}{2}×(-15)+\frac{1}{2}×0 \right\}=-\frac{5}{2}\]
になる。
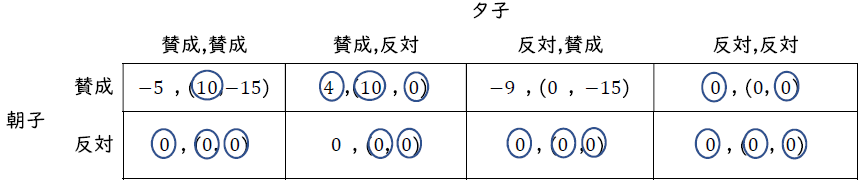
以上より利得表は以下のようになる。
利得表より(反対, 反対)がベイジアン・ナッシュ均衡である。
答え:(反対, 反対)
(別解)
(反対, 反対)がベイジアン・ナッシュ均衡であることは,反対が強支配戦略なことからも分かる。第2章の3.2節では,強支配戦略はナッシュ均衡で必ず選ばれることを学習した。ベイジアン・ナッシュ均衡は,期待利得を使うことを除いて同じ概念であるので,ベイジアンゲームにおいても,「強支配戦略はベイジアン・ナッシュ均衡で必ず選ばれる」ことが言える。そこで,本別解ではこの性質を使って解を求める。
まず,夕子も朝子も学食に行きたがっている。何故なら,美味しいか知らない状態でアモーズに行けばアモーズからの期待利得は
\[\frac{4}{10}\cdot 10+\frac{6}{10} \cdot (-15)=-5\]
なのに対して,学食からの期待利得は0であるので,学食に行く方が期待利得が高い。そして相手が賛成のときは,自分は反対することで学食に行く確率を1から1/2に低下させることができる。相手が反対している場合は,自分も反対することで,学食に行く確率を1/2から1に出来る。以上より,反対すると期待利得が高い学食に行く確率を高められので,強支配戦略となる。よって,均衡は(反対, 反対)のみである。
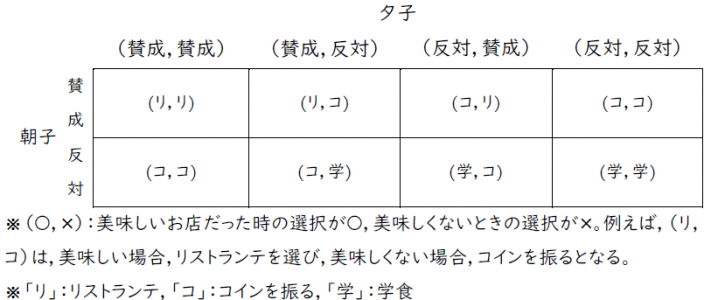
(イ) 夕子のみ学食が美味しいか否かを知っている。よって,夕子のみ行動を美味しいか否かに応じて変えることが出来る。
各戦略の組
(朝子の行動, (美味しいときの夕子の行動, 美味しくないときの夕子の行動))
に対して,利得の組
(朝子の利得, (美味しいときの夕子の利得, 美味しくないときの夕子の利得))
を求める。
例えば,(賛成, (賛成, 反対))の場合を考えよう。
- 美味しいときの夕子にとっての結果は「確率1でアモーズに行く」である。よって美味しいときの夕子の期待利得は10である。
- 美味しくないときの夕子にとっての結果は「1/2の確率でアモーズ,残りの確率で学食に行く」である。よって美味しくないときの夕子の期待利得は-15/2である。
- 朝子にとって美味しい場合の結果は「確率1でアモーズに行く」である。何故なら美味しい場合夕子は賛成するからである。一方,美味しくない場合の結果は「1/2の確率でアモーズ,残りの確率で学食に行く」である。何故なら美味しくない場合夕子は反対するからである。よって朝子の期待利得は
\[\underbrace{ \frac{4}{10} }_{美味しい確率}×10+\underbrace{ \frac{6}{10} }_{ 美味しくない確率 }×\left(-\frac{15}{2}\right)=-\frac{1}{2}\]
となる。
同じように考えると,戦略の組み合せに対する結果は,以下の通りです。
この結果に基づいて,利得を計算すると,ベイジアンゲームの利得表は以下のようになる。
利得表よりベイジアン・ナッシュ均衡は(反対, ( 賛成, 反対)) である。
答え:(反対, (賛成, 反対))
(別解)
またベイジアン・ナッシュ均衡は次のようにも求められる。まず,美味しいと知っている夕子にとっては賛成することが強支配戦略である。何故なら,夕子が反対しているなら自分は賛成することでアモーズに行く確率を\(1/2\)にでき,夕子が賛成しているなら自分も賛成することで,アモーズに行く確率を\(1\)に出来るからである。同様に,美味しくないと知っている夕子にとって反対が強支配戦略である。従って,ベイジアン・ナッシュ均衡を求めるためには,
(美味しいときの夕子の行動, 美味しくないときの夕子の行動)=(賛成, 反対)
に対する朝子の最適反応を求めれば良い。朝子は賛成を選べば
\[\frac{4}{10} \cdot 10-\frac{6}{10} \cdot \frac{15}{2}=-\frac{1}{2}\]
得るが,反対を選べば
\[\frac{4}{10} \cdot 5=2\]
を得る。よって朝子の最適反応は反対である。
(ウ)(利得表の作り方は(イ)と同様である。ただし,今回は一人でも反対すれば学食に行くので,戦略の組み合わせに対する結果は,以下のようになる。
この結果を用いて,利得表を計算すると,以下の表になる。
利得表より,ベイジアン・ナッシュ均衡は,(賛成, (賛成, 反対)) ,(反対, (賛成, 賛成)) ,(反対, (反対, 賛成)),(反対, (反対, 反対))の4つである。
答え:(賛成, (賛成, 反対)),(反対, (賛成, 賛成)),(反対(反対, 賛成)),(反対, (反対, 反対))
(別解)
また,ベイジアン・ナッシュ均衡は次のようにも求められる。まず,美味しいと知っている夕子にとって賛成は弱支配戦略である。何故なら,朝子が賛成しているとき自分の賛否で結果を変えられるので,賛成することで反対よりも高い利得が得られるが,一方で朝子が反対している時はどちらを選んでも結果は学食になるので利得は同じになるからである。同様に美味しくないと知っている夕子にとって反対は弱支配戦略である。夕子の弱支配戦略(賛成, 反対)に対して,朝子の最適反応は賛成である。よって(賛成, (賛成, 反対))はベイジアン・ナッシュ均衡である。
次に,夕子が弱く支配される戦略を取っている均衡を探す。もし,美味しいと知っている夕子と美味しくないと知っている夕子の内少なくとも一方が弱く支配される戦略を均衡で取っているならば,朝子は反対を取っていなくてはならない。そして,朝子が反対を取っているならば,美味しいと知っている夕子も美味しくないと知っている夕子も,賛成・反対どちらを選んでも利得は変わらない。従って,(反対, (賛成, 賛成)),(反対(反対, 賛成)),(反対, (反対, 反対))はベイジアン・ナッシュ均衡である。
(エ)(どのプレーヤーも弱く支配される戦略は取らないと仮定する。よって(ウ)のルールの下では (賛成, (賛成, 反対))の均衡が実現すると考える。
(ウ)のルールの方が望ましい。何故なら均衡における利得が(ウ)の方が高いからである。(イ)では(反対, (賛成, 反対))が均衡になり,利得は
(朝子の利得,(美味しいときの夕子の利得,美味しくないときの夕子の利得))=(2,5,0)
である。夕子が情報を得る前の利得に直せば,
(朝子の利得,夕子の利得)=(2,2)
である。一方(ウ)では(賛成, (賛成, 反対))が均衡になり,利得は
(朝子の利得,夕子の利得)=(4,4)
となる。
(ウ)の利得の方が高くなっている理由は,(ウ)では,どこで食べるかを情報を持っている夕子が完全に決められるからである。(ウ)のルールでは,朝子は賛成を選ぶことで情報を持っている夕子に意思決定を完全に委ねられる。具体的には,アモーズが美味しいとき,それを知っている夕子の賛成によってアモーズに行くことが決まり,美味しくない時はそれを知っている夕子の反対によって学食で食べることが決まる。一方,(イ)のルールの下では,朝子は何を選んでも,情報を持っている夕子の意見を完全には反映させられない。実際(イ)の均衡では朝子は反対しており,アモーズが本当に美味しいとき,それを知っている夕子の賛成は半分の確率でしか結果に反映されない。結果として,(ウ)のルールの方が二人にとって利得が高くなる。