交渉ゲーム

PDFファイル

【図斎　大】

1.   協力ゲーム理論と交渉ゲーム

1.1. 協力ゲーム理論とは

日本語の他の教科書の中には「協力ゲーム理論」を取り上げているものもあります。これは「ゲーム」，つまり相互依存的な状況の別の捉え方として，人々がなんらかのグループをまず作り，このグループとしての方針を決めることを前提とし，このグループとしての集団的意志決定を分析する理論です。私たちが本書で学んでいるのは「非協力ゲーム理論」というように呼ばれます。後者では独立している個々人がそれぞれの意志を決めることを前提にしています。私たちの理論でも，たとえば選挙の投票の分析（浅古，2018）のように，個々人がそれぞれの意見を表明し，それを多数決なり何らかの形で集団の意志としてまとめる状況を，ゲームとして考えることはできます。しかし協力ゲーム理論は，まず集団としてまとまった方針が決まるというのをスタートとして，そこから例えばその方針に皆が従う条件は何か，というように考えます。つまり，我々は個人からスタートし，協力ゲーム理論は集団からスタートするというのが大きな違いです。（我々の「非協力ゲーム理論」は協力と無縁なのではなく，むしろ，どのように利害が対立する人々が自発的に協力するようになるかを第６章のように一つの主なテーマと考えてきました。）

1.2. ナッシュ交渉解

私たちの非協力ゲーム理論では，モデルの「解」として様々な「均衡」を学んできました。協力ゲーム理論ではまた別の色々な，モデルの解の概念があります。その中でも，ここではナッシュ交渉解というものを取り上げます。複数の個人がこれから協力し一緒に何かを成し遂げるという状況において，その成果をどう分配すべきかという問題を考えます。具体的には以下のような例を考えましょう。

この結果としてどのような分配がなされるかというのを私たちは「解き」たいわけです。協力ゲーム理論での「解」が，以下のようなナッシュ交渉解です。

この名前にナッシュが入っているので，ナッシュ均衡のJohn Nashを思い出したかもしれません。そう，ナッシュ交渉解はナッシュ均衡とは別物なのですが，また別の論文(Nash, 1950)で，ナッシュは２社がうまく合意するために配分が満たすべき条件（公理）をいくつか挙げたうえで，それをすべて満たすなら上述の最大化問題に帰着されることを示しました。それゆえ，これにもナッシュの名前がついているのです。その公理や，それからナッシュ交渉解を導く証明については，岡田(2021，第8.２節)がとても丁寧に解説しているので，そちらを参照してください。同書の第８章は交渉ゲームでの実験や応用例も載っているので，より本格的に学びたい方にお勧めです。

上記のナッシュ交渉解では「配分として可能なもの」とあります。これをXとしましょう。我々のモデルにおいては，二者を合わせて１（兆ドル）になるような組なら何でも可能です。数学的には\(X={(x_A,x_B )∈\mathbb{R^2}| x_A+x_B≤1 }\)と書けます。ともかくこのような単純な問題で\((x_A-d_A )(x_B-d_B )\)の最大化を解くと

\[(x_A^*=d_A+\frac{1}{2} (1-d_A-d_B )，x_B^*=d_B+\frac{1}{2} (1-d_A-d_B ) \tag{NashX} \]

となります。この右辺にある\(1-d_A-d_B\)とは何でしょう。我々のモデルでは，２社がバラバラだと合わせた利益は\(d_A+d_B\)で，これは２者が協力したときの総利益１（兆ドル）より小さいとしています。経済学の用語では，新たに生み出される価値，ここでは協力することによる２社の総利益の増加を「総余剰」と呼びます。これが\(1-d_A-d_B\)なのです。上記の式は，ナッシュ交渉解に従って総利益を分配するなら，各社にまずバラバラでも成しえた利益\(d_A，d_B\)を与えたのちに，残った総余剰については等しく分けるということを意味しています。これはとても単純で，かつ対等な立場での分け方としてはもっともらしいですね。従って，ナッシュ交渉解は，たとえば国際経済学やマクロ経済学での複雑なモデルの中で，前者なら貿易協定，後者なら労使関係における利益の配分をモデル化するときに使われます。

2．ルービンシュタインの交渉ゲーム

しかし，そもそも交渉というのは，その過程自体がお互いの駆け引きになる，まさにゲームのはずです。なので，私たちの学んできた「非協力ゲーム理論」からすると，結果を天下り的に与えるだけでなく，そもそもの交渉過程を分析したいところです。そのためにはその交渉過程というのをきっちりゲームとしてモデル化しないといけません。もちろん世の中の交渉の仕方は，人・状況それぞれで，そもそも多くの場合はルールは与えられずに，手探りで力勝負なものかもしれません。（ただし，労働組合との労使交渉や，プロ野球選手の契約更改などでは，ある程度のルールはあります。）しかし，ここでは均衡における分配が結果としてナッシュ交渉解と一致するような，交渉のゲームを考えてみましょう。つまり，協力ゲーム理論における解を非協力ゲーム理論における均衡の結果として正当化することで，この二つの理論をつなげることを目標にします。ナッシュ自身もこれを課題として考えており，このような研究の方向性をナッシュ・プログラムと呼びます。

2.1. モデル

そのようなゲームとして，2者のうち片方が配分を提案，そして他方がそれを受諾するか拒否するか決め，そして拒否するなら，その拒否した方が新たな配分を提案してという交渉過程を考えます。つまり，提案する側と諾否する側が代わりばんこになるということです。このような交渉過程のゲームはAriel Rubinstein (1982)で提案されたので，ルービンシュタインの交渉ゲームと呼ばれます。

ただこれだといつまでも拒否し続けて，延々と交渉が終わらないかもしれません。なので，交渉が長くなるとお互いに損するような仕組みを入れておきます。そのために，繰り返しゲームと同じように割引因子\(β\)をモデルに組み込みます。本書での解説を思い出すと，割引因子は，将来への先延ばしがいやだという主観的な異時点間の選好から来るとも，あるいはゲームが続くことが保証されてない状況で次の期に続く確率としても解釈できるのでしたね。それはここでも同じです。つまり各プレーヤーが将来の利益を割り引いて計算するのだとも，あるいは交渉が決裂する確率としても解釈できます。ここでは後者で解釈し，そして決裂した場合には，各社は\(d_A,d_B\)を得るものだとしましょう。

均衡を数学的に解く前に，どのようになるのか予想を直感で立てておきましょう。受諾か拒否か決める受け手の立場でのそれぞれの選択肢から得られる利益は何でしょう。いまの提案を受諾しておけば，その提案通りの利得は確保できます。他方で，拒否すると，翌朝には自分が提案する側になりますが，そもそも交渉が決裂してしまう可能性もあります。つまり，妥協と交渉決裂のトレードオフに受け手は直面しています。もちろん提案された案で受け手への分配が多ければ妥協するインセンティブが大きく，それが少なければ決裂してでも提案権を取ろうとするインセンティブが大きくなります。この間に，受諾するか拒否するかの境目がありそうです。そして，提案する側としては，もちろん自分の取り分を大きくはしたいので，受け手が受諾してくれそうなギリギリのところを提案したいでしょう。この駆け引きはまさにゲームです。

さて，均衡はどうなるでしょう。私たちの（非協力）ゲーム理論における均衡とは，要するに，戦略が自己拘束的で，かつその背後にある予想が事後整合的である状態のことでした。後者はこの話の中で言えば，提案者の方も結局は受け手のほうがどんな提案なら受諾してくれるのか，とくにそのギリギリの分配を正しく予想できているということです。ならば，提案者はまさにこのギリギリの分配ぴったりを提案して，残りをごっそりもらってしまえばよいわけです。そして，この予想は正しいので，受け手はそれを受諾することになるというわけです。というと，提案者が有利，特に先に提案権を取るアボカドが有利になり，均衡の結果としても多く利益を取りそうですね。実際，それでナッシュ均衡にはなることを，これから具体的に均衡での分配を計算しながら確かめます。この先手有利の分だけ，総余剰を等しく分けるナッシュ交渉解からずれているのですが，そんなに離れていないことも計算から見えてきます。

2.2. 定常戦略の均衡

ルービンシュタインの交渉ゲームは無限繰り返しゲームと似ているところがあります。まず，終わりが定まっていないので，後ろ向き帰納法が使えないこと。そして，利得が割り引かれ，提案者が日ごとに交替しているけれども，そのことを除けば毎日が同じことの繰り返しになっていること。つまり，提案者・受け手という立場については，どの日も同じ選択であり，また割り引く前の利得を考えれば，それぞれの選択のもたらす利得は同じになっています。

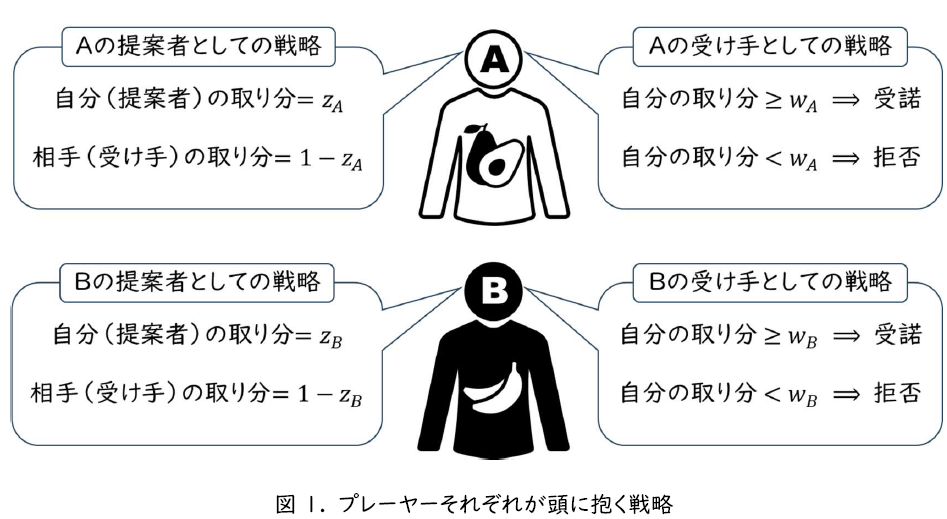
この同じような交渉が続くという点に注目すると，各プレーヤーが提案者，受け手それぞれの立場に立った時には，それが何日目かによらない，同じ選択をしても均衡ではおかしくないでしょう。つまり，均衡では，どの期も（せいぜい自分が提案する側か受け手側かの違いだけで）同じ配分案が提案されるでしょう。あと，受け手のほうとしては，自分の取り分が十分高ければ受諾するし，低ければ拒否するというのが自然で，その境目となる受け手の取り分というのが，どの期でも同じになるでしょう。このような戦略を定常戦略と呼びます。以下では，自分が提案する側なら，自分に\(z\), 相手（受け手）に\(1-z\)を分配することを提案するという戦略を考えます。また，自分が受け手なら，自分にwのシェア以上が来るかどうかで受諾・拒否を決めるという戦略，つまりwが受諾するギリギリの受け手の分配だという戦略を受け手について考えます。その上で，これが均衡になるような\(z\)と\(w\)の値を求めていきます。そのためには事後整合的な予想を持っているという前提のもとに，各プレーヤーがそれぞれの立場におけるzとwの選択が最適となる条件を見ていきます。ただ我々の予想では，先手のアボカドが有利になりそうなので，プレーヤーごとに\(z\)と\(w\)は異なるかもしれません。なので，アボカドのA，バナナのBを\(z_A\)，\(z_B\)のように\(z，w\)の添え字に付けて区別しましょう。

まずは受け手側，特にアボカドが受け手の立場に立った時の最適条件から考えてみましょう。バナナから提案者ということですが，その提案の配分の中で\(z_B\)がバナナ自身への配分でした。つまり，アボカドへは\(1-z_B\)の配分が提案されたことになります。均衡においてこの配分を受諾するのが最適であるということは， この配分を確実にもらうことの利得が，拒否して先延ばしすることによる期待利得を上回るということです。後者がなぜ「期待」かというと，確率\(β\)で来期に交渉が続き自分が提案者になり（均衡においては）受諾されるギリギリの提案を出し，提案者としての利得\(z_A\)を得られる一方で，確率\(1-β\)でそもそも交渉が決裂し，\(d_A\)しか得られなくなるからです。まとめると，Aにとっては拒否することの期待利得は\(βz_A+(1-β) d_A\)となります. 提案者であるBがこれよりも多くAに利益を分配するなら，Aにその提案を受諾してもらえます。従って，Aに受諾してもらうためのギリギリの分配\(w_A\)というのは，この拒否による期待利得ちょうどを与えるものとなります。すなわちAが受諾するかどうかの境目として最適なのは，\(w_A=βz_A+(1-β) d_A\)です。Bが受け手だとしても，同様に\(w_B=βz_B+(1-β) d_B\)となります。以上をまとめると

\[w_A=βz_A+(1-β) d_A，w_B=βz_B+(1-β) d_B　\tag{Eqm1} \]

という受け手側の均衡条件を一つ得ます。

さて，提案する側を考えてみましょう。こちらは自分の取り分を多くしたいので，以上の\(w_A，w_B\)が事後整合的に予想されるという前提の下では，相手へ提案する配分を相手の受けるギリギリにするのが最適です。Aが提案者ならば，受け手Bへの配分\(1-z_A\)をBの受けるギリギリの\(w_B\)に設定します。つまり，Aにとって最適な提案は\(1-z_A=w_B\)となります。同様にBが提案者であるときに，最適な提案は\(1-z_B=w_A\)となります。以上より

\[1-z_A=w_B，1-z_B=w_A \tag{Eqm2} \]

という提案者側の均衡条件を一つ得ます。

この(Eqm2)を(Eqm1)に代入すると

\[1-z_A=βz_B+(1-β) d_B，1-z_B=βz_A+(1-β) d_A\]

を得ます。それぞれの式を変形していくと前者は\(z_A+βz_B=1-(1-β) d_B\)，後者は\(z_B+βz_A=1-(1-β) d_A\)となります。この両辺を足し合わせると\((1+β)(z_A+z_B )=2-(1-β)(d_A+d_B )\)を，また各辺の差を取ると\((1-β)(z_A-z_B )=(1-β)(d_A-d_B )\)を得ます。つまり，\(z_A\)と\(z_B\)の和と差について，

\[z_A+z_B=d_A+d_B+\frac{2}{1+β}(1-d_A-d_B)， z_A-z_B=d_A-d_B\]

を得ます。これらをともに満たす解を\((z_A^⋕，z_B^⋕)\)とおくと，

\[z_A^⋕=d_A+\frac{1}{1+β} (1-d_A-d_B )，z_B^⋕=d_B+\frac{1}{1+β} (1-d_A-d_B) \tag{EqmZ} \]　

と求められます。更に（Eqm2）にこれを代入して，\(w\)についての解を\((w_A^⋕,w_B^⋕)\)とすると，

\[w_B^⋕=1-z_A^⋕= d_B+\frac{β}{1+β} (1-d_A-d_B )，w_A^⋕=1-z_B^⋕= d_A+\frac{β}{1+β} (1-d_A-d_B ) \tag{EqmW} \]　

を得ます。

提案者が(EqmZ)の定常戦略に従って分配案を提案するならば，受け手への分配は(EqmW)に求められた受諾するギリギリなので，受け手はそれを受諾することになり，そして交渉は終結します。このモデルではアボカドが初日Day 0に提案権を得るので，アボカドが(EqmZ)の第１式どおりの\(z_A\)を自分に，そして\(1-z_A\)を相手に分配することを提案します。そして，受け手となるバナナにとっては，この\(1-z_A\)は(EqmW)の第１式どおりの\(w_B\)と一致するので，この提案を受諾します。結果として交渉はDay 0で早々と終わります。すなわち，この均衡の定常戦略に従って実現する分配を\((x_A^⋕，x_B^⋕)\)とおくと，

\[x_A^⋕=z_A^⋕=d_A+\frac{1}{1+β} (1-d_A-d_B )，x_B^⋕=w_B^⋕= d_B+\frac{β}{1+β} (1-d_A-d_B ) \tag{#X} \]

となります。

つまり，総余剰については，アボカドとバナナとで\(1:β\)の比で分け合うことになります。\(β<1\)なので先に予想した通り，先手となるアボカドのほうが総余剰を多く受け取り， 優位であることがわかります。ただ，\(β\)が大きくなり１に近づくほど，この比は1:1に，つまり等しく総余剰を分けるのに近づいていきます。割引因子\(β\)は交渉が続く確率でした。これが１より小さいとアボカドが優位ということは，先手の優位さが交渉が決裂する可能性によるものであって，その可能性が小さくなるほど先手と後手の差がなくなることを示唆しています。

この均衡での分配(EqmX)とナッシュ交渉解(NashX)とを比べると，まさにこの\(β\)が１になる極限で前者が後者と一致することが見て取れます。従って，ナッシュ交渉解は，たしかにルービンシュタインの交渉ゲームにおける均衡の配分で，特に交渉決裂の可能性がなくなっていく極限として正当化できます。すなわち，現実の交渉を考えたり，交渉を組み込んだモデルの中でナッシュ交渉解を使うことは，協力を前提としなくても，このような交渉過程の結果としてとらえられるということです。

2.3. 無限でのSPE再び

ところでこの「均衡」はどの均衡でしょう？同時手番ゲームではないので部分ゲーム完全均衡を考えます。このルービンシュタインの交渉ゲームはまさに，完全情報の逐次手番ゲームです。夜に手番が来る受け手には，これまでの選択，特に朝に提案者がどんな分配案を選んできたかは見えています。朝に手番が来る提案者もやはり，これまでの選択，特に前の晩にそのときの受け手（自分）が拒否していたこと，そしてその朝にどんな提案がされたかは見えています。なので，完全情報になっています。

それでは部分ゲームは何でしょう？逐次手番なので，提案者の手番である朝，受け手の手番である夜のそれぞれで新しい部分ゲームが始まります。つまり，各日において，その朝から先の全体がひとつの新たな部分ゲームを成し，またその朝になんらかの分配案が出された後の夜から，またそれから先の全体がひとつの新たな部分ゲームを成します。

どうやって(EqmZ),(EqmW)で求めた定常戦略の組が部分ゲーム完全均衡になると証明できるのでしょう？先述の通り，無限に続くということは，後ろ向き帰納法が使えません。なので，原則的には，部分ゲーム完全均衡の定義に立ち戻り，２社のこの定常戦略の組が部分ゲームのそれぞれでナッシュ均衡を導き出すことを示すことになります。つまり，どんな部分ゲームにおいても，どのプレーヤーについても，自分だけ(EqmZ),(EqmW)で求めた定常戦略からどのように逸脱したとしても，利得をより高くすることはできないということを示さないといけません。部分ゲームとしてどこかで始まるものをひとつ取っても，その先に無限に続く朝夜のどこでも，またその中の何回でも逸脱はあり得るので，このままでは定常戦略と比べるべき逸脱の戦略は途方もなく無限にあることになります。私たちも途方に暮れてしまいますね。

しかし幸いなことに，無限繰り返しゲームと同様に，ルービンシュタインの交渉ゲームでも一回逸脱原理がやはり成立することが知られています。（それを明示した教科書的な説明として，英語ですがOsborne (2004, Sec.16.1)のProposition 471.4を参照。）つまり，部分ゲーム完全均衡を示すためには無限にありえる逸脱戦略すべてを考えなくても，各部分ゲームにおいて，そのスタートにおいてだけ選択を変えるという一回逸脱の戦略だけ考えて，それが利得を高くしないことさえ証明すれば十分だというわけです。

この一回逸脱原理に従って，(EqmZ),(EqmW)の定常戦略の組が部分ゲーム完全均衡になっていることを示しましょう。まずは，無限にありえる部分ゲームを，わたしたちが分析しきることのできるよう，いくつかのケースに分類しましょう。ちなみに，この部分ゲームは，まず起点となる日が無限にあること，そしてそれまでの提案も（どんな分配の比でもいいので）無限個あり，そしてその履歴ごとに異なる部分ゲームとして数えるので，本当にたくさんありえます。これをどう分類すればよいでしょう。

まず，各日の朝をスタートとする部分ゲームですが，朝になれば新たな提案ができるので，ともかく交渉がこの朝まで続いていること以外の，それまでにどんな提案があったとかの履歴はどうでもよいでしょう。，（それは定常戦略自体が，今日が何日目か，そしてこれまでの履歴がどうだったかということに左右されないものであるということも効いています。）なので，朝の部分ゲームはひとまとめにして分析できるはずです。実際，そうしたことに左右されずに，均衡の候補である(EqmZ), (EqmW)の戦略や一回逸脱の戦略それぞれがもたらす利得は以下のように計算できます。以下では取り合えずアボカドを提案者とし，その提案する配分を\((z_A，1-z_A)\)とします。

a)　(EqmZ)の戦略どおり\(z_A=z_A^⋕\)の提案をしたとき。これはその夜に受け手のバナナが受諾してくれるので，提案者自身は(EqmZ) の提案ちょうどの利得を得ます。例えばこの提案者がアボカドなら\(z_A^⋕=d_A+\frac{1}{1+β} (1-d_A-d_B)\)を得るということになります。

b)　(EqmZ)よりも受け手に多くを与える提案へ一回逸脱した，つまり\(1-z_A \gt 1-z_A^⋕\)であるとき。(EqmZ)での\(1-z_A^⋕\)は受け手の受諾するギリギリであり，それよりも\(1-z_A\)は多いので，この提案はやはり受諾されます。従って，この提案通りの配分\(z_A\)を提案者はもらうことになります。しかし相手に譲っているだけ自分への配分は\(z_A^⋕\)より小さくなるのでもちろん損しています。つまり，a)のときよりも，この逸脱からの利得は低くなります。受諾されるのなら譲歩しない方が提案者にはよいのは自然ですね。

c)　(EqmZ)よりも自らに多く与える提案へ一回逸脱した，つまり\(z_A \gt z_A^⋕\)であるとき。(EqmZ)での\(1-z_A^⋕\)が受け手であるバナナの受諾するギリギリで，この提案での受け手への分配\(1-z_A\)はそれよりも少ないということになります。なので，この提案は拒絶されます。一回逸脱原理によれば，次でバナナは定常戦略どおりの提案\(z_B^⋕\)を出し，アボカドはそれを受諾することになります。つまり，翌日にアボカドは受け手として(EqmW)どおり\(1-z_B^⋕=w_B^⋕\)の利得を得ることになります。ただし日をまたぐときに確率\(1-β\)で交渉は決裂しえたので，提案者だった日における期待利得としては

\[βw_A^⋕+(1-β) d_A=β{d_A+\frac{β}{1+β} (1-d_A-d_B )}+(1-β) d_A=d_A+\frac{β^2}{1+β} (1-d_A-d_B)\]

となります。

提案者として一回逸脱を選ばないための条件は，c)のときの利得がa)のときの利得を上回らないということになります。提案者がアボカドだとすると，それはすなわち

\[d_A+\frac{β^2}{1+β} (1-d_A-d_B ) ≤ d_A+\frac{1}{1+β} (1-d_A-d_B )\]

ということです。\(1>d_A+d_B\)なので，この式は\(β^2≤1\)に帰着されます。\(β<1\)なのでこれは常に満たされます。提案者がバナナでも以上の議論は当てはまり，やはり\(β<1\)でさえあれば一回逸脱が得になることはありません。

次に，受け手で始まる夜からの部分ゲームを考えましょう。受け手の利得について，拒否したときの利得は，一回逸脱原理に従うと翌朝には(EqmZ)どおりの分配案を自ら提案できるので，どの部分ゲームでも同じになります。そしてそれは結局受諾されます。すなわち拒否したときには，翌日に交渉が続く限りは(EqmZ)で提案するとおりの分配を取れることになります。ただ翌日まで続かず，交渉が決裂する可能性も，拒否したときの利得の計算にいれなくてはいけません。従って，この受け手がアボカドだとすると，拒否したときの利得は

\[βz_A^⋕+(1-β) d_A=β{d_A+\frac{1}{1+β} (1-d_A-d_B )}+(1-β) d_A=d_A+\frac{β}{1+β} (1-d_A-d_B )\]

となります。これは\(w_A^⋕\)と等しいですね。実際，(Eqm1)で拒否したときの結果の利得と等しくなるように，この境目は決めたのでした。他方で，提案を受諾したときの利得は，その前の朝に提案者が出した配分案に依存します。なので，どんな提案だったかによって，この夜からの部分ゲームを更に場合分けしましょう。以下では，アボカドが受け手だとしましょう。

a)提案された分配案が(EqmZ)の定常戦略どおりだったとき。受け手の方も(EqmW)どおりに諾否の境目をおく定常戦略に従うなら受諾することになります。そうすると\(1-z_B^⋕\)を確実にもらえることになります。これは\(w_A^⋕\)と等しかったのですよね。なので，拒否するのと等しい，どっこいどっこいの利得ということになります。つまり受け手はわざわざここで拒否に一回逸脱しても，利得を増やしはしないということです。

b) 提案された分配案が(EqmZ)の定常戦略よりも，受け手に多く分配するものだったとき。つまり，\(1-z_B^⋕\)よりも多い分配を提案してくれているので，受け手の方は(EqmW)どおりに諾否の境目をおく定常戦略に従うなら受諾することになります。そうすると，提案された分配が\(1-z_B^⋕=w_A^⋕\)よりも大きい分だけ，\(w_A^⋕\)より大きな利得を得ることになります。この\(w_A^⋕\)が拒否したときの利得だったのですから，この場合には拒否に一回逸脱すると，むしろ利得が減ってしまうことになります。

c) 提案された分配案が(EqmZ)の定常戦略よりも，受け手に少なく分配するものだったとき。つまり，\(1-z_B^⋕=w_A^⋕\)よりも少ない分配を提案しているので，受け手の方は(EqmW)どおりに諾否の境目をおく定常戦略に従うなら拒否することになります。そのことによる期待利得が\(w_A^⋕\)になるのでした。他方で，もしもこの提案を受諾してしまうと，提案された分配が\(1-z_B^⋕=w_A^⋕\)よりも少ない分だけ，\(w_A^⋕\)より小さな利得を得ることになります。従って，この場合に受諾に一回逸脱すると，むしろ利得が減ってしまうことになります。

ここまでの分析は2.2節での（Eqm1）や（Eqm1）の議論をなぞっているように見えるかもしれません。しかしここでは，a)で見た境目で受諾するオファーの境目の値を求めようというだけでなくて，きちんとその境目の外のb),c)の場合にそれぞれ受諾，拒否をするのがよいということも確認しています。つまり，あらゆる部分ゲームのあらゆる場合で，どちらのプレーヤーも★からの一回逸脱をするインセンティブがないことを確認しているわけです。なので★は部分ゲーム完全均衡だと言えます。

２.４. 有限にしたり人数増やしたりすると？

ちなみに本書の繰り返しゲームでは有限と無限とで結果が大きく異なりました。このオンライン・コンテンツでの交渉ゲームに関しては，実は有限にしてもあまり結果は変わりません。交渉ゲームで有限にしか続かないとは，交渉に締め切りとなる「最後の期」があって，そこまでにまとまらなければ容赦なく交渉は打ち切られ，各プレーヤーは\(d_A，d_B\)を受け取るしかないという状況です。もちろんこの締め切りが短いと，先手の優位さが強まります。しかし締め切りが延びれば延びるほど，無限での結果，つまり(EqmX)の配分に近づいていきます。ただ無限では今が何期目だろうと利得の構造は同じになることから定常戦略で均衡の配分を求められましたが，有限になると何期目なのかというのが無視できません。他方で，「最後の期」があるので，後ろ向き帰納法によって，最後から１期ずつ各プレーヤーの戦略を求めることになります。その解き方をきちんと見てみたい方は，やはり岡田(2021)やOsborne (2004)で詳しく解説しているので参照してください。

２人から３人以上にするのも自然と興味がわくでしょう。ナッシュ交渉解については，３人目をCと表せば，このプレーヤーについても\(x_C≥ d_C\)を満たすような配分のうち，\((x_A-d_A)(x_B-d_B)(x_C-d_C)\)を最大にするものとして定義されます。そしてそれは，みんなが定常戦略を取る部分ゲーム完全均衡について，交渉が続く確率\(β\)が１に近づいたときの配分として正当化されます。ただし，３人以上になると，定常戦略を取らないような部分ゲーム完全均衡も存在します。これは洋書であり，また非常に簡潔な分だけ抽象度が高いことで知られるOsborne & Rubinstein　(1994, pp.130-131)で触れられています。この本は著者であるAriel Rubinsteinのホームページからタダで手に入るので，そのような沼にはまってみたい方はチャレンジしてみてください。

複数の均衡があるとなると，やはり進化の過程でどのような均衡が生き残るのかが気になりますね。実は，同時手番でないゲームについては，そもそも部分ゲーム完全均衡に進化の行く末を絞り込んでいいのかということ自体が，あまり簡単なことではありません。ひとつの大きな問題は，部分ゲーム完全均衡では実際にプレーしていない仮想的な部分ゲームも先読みして合理性を課していることに対して，最適反応動学のような進化動学では実際のプレーでの利得の大小で戦略が淘汰されるというところに，大きなギャップがあります。これを埋めるのが，より大きな利得へと適応するのと別に，その場では利得が必ずしも高くはならない戦略を試してみる試行錯誤・突然変異を盛り込む，確率進化というアイデアです。交渉ゲームにおける進化に関して，このアイデアの下でたくさんの研究が蓄積されています。それについては確率進化の理論の勉強とともに，Sandholm (2010)のIntroductionの末尾で列挙されている文献を参考するとよいでしょう。

参考文献

• 浅古泰史（2018）『ゲーム理論で考える政治学』有斐閣
• 岡田章（2021）『ゲーム理論』第３版，有斐閣
• Nash, John F., Jr. (1950). “The bargaining problem”. Econometrica. 18 (2): 155–162.
• Osborne, Martin J. (2004). An Introduction to Game Theory. Oxford University Press.
• Osborne, Martin J. & Rubinstein, Ariel (1994). A Course in Game Theory. MIT Press．https://arielrubinstein.tau.ac.il/ で無料で配布
• Rubinstein, Ariel (1982). “Perfect Equilibrium in a Bargaining Model”. Econometrica. 50 (1): 97–109.