【小俵将之・浅古泰史・森谷文利・図斎大】
問題4.1(均衡の安定性)
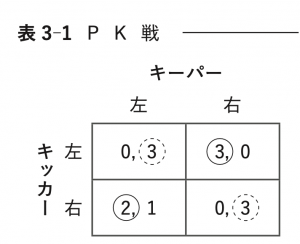
ⅰ.PK戦(表3-1)
利得表は以下である。キッカーが左を選ぶ確率\(p\)を,キーパーが左を選ぶ確率\(q\)をとする。
(ア)第3章3節を振り返ると,両プレーヤーの最適反応は以下の通りだった。
- キッカーの最適反応
- \(q \lt 6/10\)ならばキッカーは\(p=1\)のみが最適反応
- \(q=6/10\)ならばキッカーは\(p\)が\(0\)から\(1\)のどれでも最適反応
- \(q>6/10\)ならばキッカーは\(p=0\)のみが最適反応
- キーパーの最適反応
- \(p>4/10\)ならばキーパーは\(q=1\)のみが最適反応。
- \(p=4/10\)ならばキーパーは\(q\)が\(0\)から\(1\)のどれでも最適反応。
- \(p \lt 4/10\)ならばキーパーは\(q=0\)のみが最適反応。
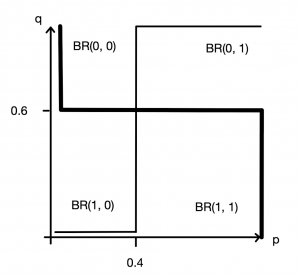
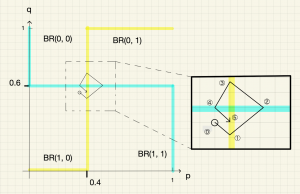
よって最適反応は以下のように図示できる。太線はキッカーの,細線はキーパーの最適反応である。
ナッシュ均衡は\((p^*,q^* )=(0.4,0.6)\)である。
(イ)ずらした4つの初期状態全てで,ナッシュ均衡\(\boldsymbol{(p^*,q^* )=(0.4,0.6)}\)に収束する。
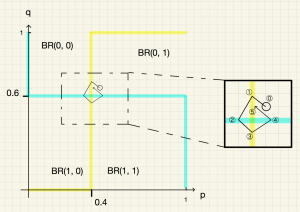
初期状態が\(\boldsymbol{(p^*+0.05,q^*+0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=0\)と\(q=1\)なので,\((p,q)\)は初期状態から左上隅の\((0,1)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置①)。このとき,最適反応は\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置②)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置③)。このとき,最適反応は\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=0\)と\(q=1\)に切り替わるので,\((p,q)\)は左上隅の\((0,1)\)に向かって進む。そして,再びキーパーの最適反応のグラフ\(p=0.4\)にぶつかる(位置⑤)。
以上のように,初期状態の向かう先は
\[\underbrace{ (0,1) → (0,0) → (1,0) → (1,1) }_{ ⓪→①→②→③→④ }→\underbrace{ (0,1) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると⑤の方がナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に収束する。
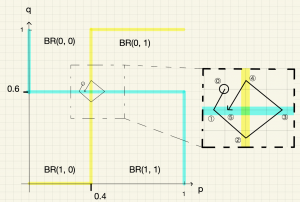
初期状態が\(\boldsymbol{(p^*-0.05,q^*+0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=0\)と\(q=0\)なので,\((p,q)\)は初期状態から左下隅の\((0,0)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置①)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置②)。このとき,最適反応は\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置③)。このとき,最適反応は\(p=0\)と\(q=1\)に切り替わるので,\((p,q)\)は左上隅の\((0,1)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。そして,再びキッカーの最適反応のグラフ\(q=0.6\)にぶつかる(位置⑤)。
以上のように,初期状態の向かう先は
\[\underbrace{ (0,0) → (1,0) → (1,1) → (0,1) }_{ ⓪→①→②→③→④ }→\underbrace{ (0,0) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると⑤の方がナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に収束する。
初期状態が\(\boldsymbol{p^*-0.05,q^*-0.05}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=1\)と\(q=0\)なので,\((p,q)\)は初期状態から右下隅の\((1,0)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置①)。このとき,最適反応は\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置②)。このとき,最適反応は\(p=0\)と\(q=1\)に切り替わるので,\((p,q)\)は左上隅の\((0,1)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置③)。このとき,最適反応は\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。そして,再びキーパーの最適反応のグラフ\(p=0.4\)にぶつかる(位置⑤)。
以上のように,初期状態の向かう先は
\[\underbrace{ (1,0) → (1,1) → (0,1) → (0,0) }_{ ⓪→①→②→③→④ }→\underbrace{ (1,0) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると⑤の方がナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に収束する。
初期状態が\(\boldsymbol{(p^*+0.05,q^*-0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=1\)と\(q=1\)なので,\((p,q)\)は初期状態から右上隅の\((1,1)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置①)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は左上隅の\((1,0)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置②)。このとき,最適反応は\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。すると,キッカーの最適反応のグラフ\(q=0.6\)を通り過ぎる(位置③)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。すると,キーパーの最適反応のグラフ\(p=0.4\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。そして,再びキッカーの最適反応のグラフ\(q=0.6\)にぶつかる(位置⑤)。
以上のように,初期状態の向かう先は
\[\underbrace{ (1,1) → (0,1) → (0,0) → (1,0) }_{ ⓪→①→②→③→④ }→\underbrace{ (1,1) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると,⑤の方がナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に収束する。
(ウ)以上の議論をまとめると,どの領域からスタートしても最適反応動学は以下の二つを繰り返す。
- \(p=0.4\)にぶつかり,キーパーの最適反応が切り替わり,\(q\)の動く向きが逆になることで\(q=0.6\)に戻ってくる。
- \(q=0.6\)にぶつかり,キッカーの最適反応が切り替わり,\(p\)の動く向きが逆になることで\(p=0.4\)に戻ってくる。
そして\((p,q)\)は螺旋を描いてナッシュ均衡\((p^*,q^* )=(0.4,0.6)\)に収束する。これは初期状態がどこにあったかに依らないので,ナッシュ均衡\(\boldsymbol{(p^*,q^* )=(0.4,0.6)}\)は大域的に安定であると言える。
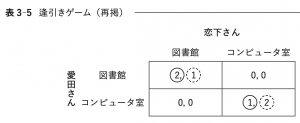
ⅱ.逢引きゲーム(表3-5)
愛田さんが図書館を選ぶ確率を\(p\),恋下さんが図書館を選ぶ確率を\(q\)とする。
(ア) 第3章4節を振り返ると,両プレーヤーの最適反応は以下の通りだった。
- 愛田さんの最適反応
- \(q>1/3\)ならば愛田さんは\(p=1\)のみが最適反応。
- \(q=1/3\)ならば愛田さんは\(p\)が\(0\)から\(1\)のどれでも最適反応。
- \(q \lt 1/3\)ならば愛田さんは\(p=0\)のみが最適反応。
- 恋下さんの最適反応
- \(p>2/3\)ならば恋下さんは\(q=1\)のみが最適反応。
- \(p=2/3\)ならば恋下さんは\(q\)が\(0\)から\(1\)のどれでも最適反応。
- \(p \lt 2/3\)ならば恋下さんは\(q=0\)のみが最適反応。
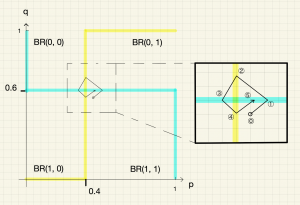
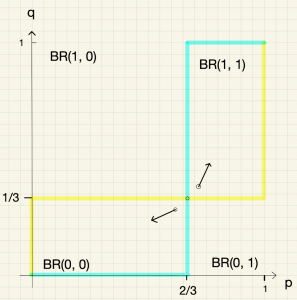
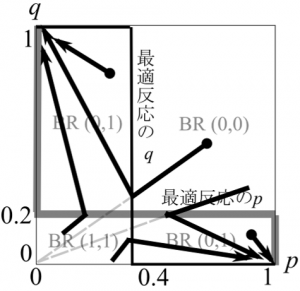
よって最適反応は以下のように図示できる。太線が愛田さん,細線が恋下さんの最適反応である。
ナッシュ均衡は\((p,q)=(0,0),(2/3,1/3),(1,1)\)の3つである。
(イ)ナッシュ均衡\(\boldsymbol{(2/3,1/3)}\)
ケース1a. \((2/3+0.05,1/3+0.05)\)を初期状態とする。つまり\((2/3,1/3)\)の右上を初期状態とする。ここにおける最適反応は\(p=1\)と\(q=1\)なので,初期状態は\((1,1)\)に向かって進む。この移動の過程では誰の最適反応も切り替わらないので,このまま\((1,1)\)に収束する。\((1,1)\)はナッシュ均衡なのでここからは動かない。
\((2/3-0.05,1/3-0.05)\)を初期状態とする。つまり\((2/3,1/3)\)の左上を初期状態とする。ここにおける最適反応は\(p=0\)と\(q=0\)なので,初期状態は\((0,0)\)に向かって進む。この移動の過程では誰の最適反応も切り替わらないので,このまま\((0,0)\)に収束する。\((1,1)\)はナッシュ均衡なのでここからは動かない。
まとめると,初期状態がナッシュ均衡\((2/3,1/3)\)の右上もしくは左下ならば元の均衡には戻らない。右上の場合\((1,1)\)に収束し,左下ならば\((0,0)\)に収束する。下図を参照。
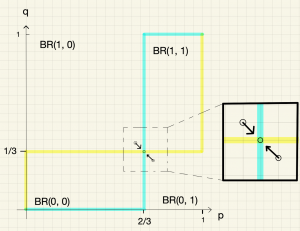
ケース1b. \((2/3-0.05,1/3+0.05)\)を初期状態とする。つまり\((2/3,1/3)\)の左上を初期状態とする。ここにおける最適反応は\(p=1\)と\(q=0\)である。よって\((p,q)\)は初期状態と\((1,0)\)を結んだ直線上を沿って\((1,0)\)に向かって進む。元のナッシュ均衡\((2/3,1/3)\)はこの直線上に存在するので,誰の最適反応も切り替わらずに再び元のナッシュ均衡に収束する。
\((2/3+0.05,1/3-0.05)\)を初期状態とする。つまり\((2/3,1/3)\)の右下を初期状態とする。ここにおける最適反応は\(p=0\)と\(q=1\)である。よって\((p,q)\)は初期状態と\((0,1)\)を結んだ直線上を沿って\((0,1)\)に向かって進む。元のナッシュ均衡\((2/3,1/3)\)はこの直線上に存在するので,誰の最適反応も切り替わらずに再び元のナッシュ均衡に収束する。
まとめると,初期状態がナッシュ均衡\((2/3,1/3)\)の左上もしくは右下ならば元の均衡に戻る。下図を参照。
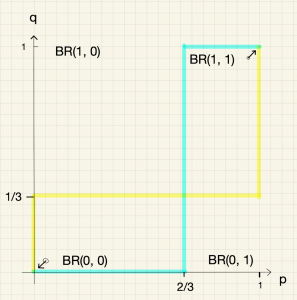
ナッシュ均衡\(\boldsymbol{(0,0)}\)とナッシュ均衡\(\boldsymbol{(1,1)}\)
ケース2. ナッシュ均衡\((0,0)\)については,\((0+0.05,0+0.05)\)を初期状態とした場合,最適反応は\(p=0\)と\(q=0\)なので再びナッシュ均衡に収束する。
ケース3. ナッシュ均衡\((1,1)\)も,\((1-0.05,1-0.05)\)を初期状態とした場合,最適反応は\(p=1\)と\(q=1\)なので再び元のナッシュ均衡に収束する。下図を参照。
(ウ)ナッシュ均衡\(\boldsymbol{(2/3,1/3)}\) (イ)のケース1aでの議論を振り返ると,ナッシュ均衡\((2/3,1/3)\)から左下に少しでもずれると,最適反応がずっと\(p=0\)と\(q=0\)のまま\((0,0)\)へと収束してしまう。(同様にケース1bを振り返ると,右上に少しでもずれると\((1,1)\)へと収束してしまう。)従って,\((2/3,1/3)\)からずれる方向によってはどんなに近かったとしても元の均衡には収束しない。従って,このナッシュ均衡\((2/3,1/3)\)は不安定である。
ナッシュ均衡\((0,0)\). 初期状態が\(p \lt 2/3\)かつ\(q \lt 1/3\)の範囲,つまり\((2/3,1/3)\)の左下ならば,\((0,0)\)からどんな方向にずれていても,最適反応がずっと\(p=0\)と\(q=0\)のまま\((0,0)\)へと収束する。従って,このナッシュ均衡\((0,0)\)は安定である。
ナッシュ均衡(1,1). 初期状態が\(p>2/3\)かつ\(q>1/3\)の範囲,つまりの\((2/3,1/3)\)の右上ならば,\((1,1)\)からどんな方向にずれていても,最適反応がずっと\(p=1\)と\(q=1\)のまま\((1,1)\)へと収束する。従って,このナッシュ均衡\((1,1)\)は安定である。
大域的に安定なナッシュ均衡は存在しない。(イ)のケース2とケース3を比べると,全ての初期状態の収束先となっているようなナッシュ均衡は存在しないと言える。
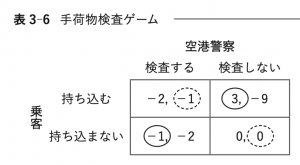
ⅲ.手荷物検査ゲーム(表3-6)
乗客が「持ち込む」を選ぶ確率を\(p\),空港警察が検査する確率を\(q\)とする。
(ア)第3章5節を振り返ると,両プレーヤーの最適反応は以下の通りだった。
- 乗客の最適反応
- \(q \lt 0.75\)ならば乗客は\(p=1\)のみが最適反応。
- \(q=0.75\)ならば乗客さんは\(p\)が\(0\)から\(1\)のどれでも最適反応。
- \(q>0.75\)ならば乗客さんは\(p=0\)のみが最適反応。
- 空港警察の最適反応
- \(p>0.2\)ならば空港警察は\(q=1\)のみが最適反応。
- \(p=0.2\)ならば空港警察は\(q\)が\(0\)から\(1\)のどれでも最適反応。
- \(p \lt 0.2\)ならば空港警察は\(q=0\)のみが最適反応。
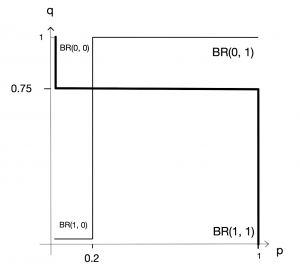
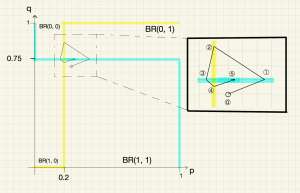
よって最適反応は以下のように図示できる。太線が乗客,細線が空港警察の最適反応である。
ナッシュ均衡は\((p^*,q^* )=(0.2,0.75)\)のみである。
(イ)ずらした4つの初期状態全てで,ナッシュ均衡\(\boldsymbol{(p^*,q^* )=(0.2,0.75)}\)に収束する。
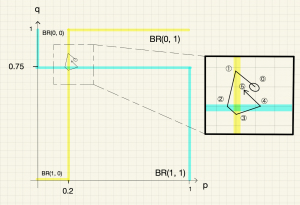
初期状態が\(\boldsymbol{(p^*+0.05,q^*+0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=0\)と\(q=1\)なので,\((p,q)\)は初期状態から左上隅の\((0,1)\)に向かって進む。すると,空港警察の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置①)。このとき,最適反応は\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。すると,乗客の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置②)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。すると,空港警察の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置③)。このとき,最適反応は\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。すると,乗客の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=0\)と\(q=1\)に切り替わるので,\((p,q)\)は左上隅の\((0,1)\)に向かって進む。そして,再びの空港警察最適反応のグラフ\(p=0.2\)にぶつかる(位置⑤)。
以上のように,初期状態の向かう先は
\[\underbrace{ (0,1) → (0,0) → (1,0) → (1,1) }_{ ⓪→①→②→③→④ }→\underbrace{ (0,1) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると⑤の方がナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に収束する。
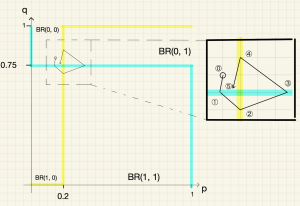
初期状態が\(\boldsymbol{(p^*-0.05,q^*+0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=0\)と\(q=0\)なので,\((p,q)\)は初期状態から左下隅の\((0,0)\)に向かって進む。すると,空港警察の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置①)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。すると,乗客の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置②)。このとき,最適反応は\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。すると,空港警察の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置③)。このとき,最適反応は\(p=0\)と\(q=1\)に切り替わるので,\((p,q)\)は左上隅の\((0,1)\)に向かって進む。すると,乗客の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。そして,再び空港警察の最適反応のグラフ\(q=0.75\)にぶつかる(位置⑤)
以上のように,初期状態の向かう先は
\[\underbrace{ (0,0) → (1,0) → (1,1) → (0,1) }_{ ⓪→①→②→③→④ }→\underbrace{ (0,0) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると⑤の方がナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に収束する
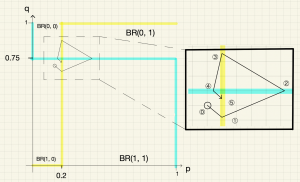
初期状態が\(\boldsymbol{(p^*-0.05,q^*-0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=1\)と\(q=0\)なので,\((p,q)\)は初期状態から右下隅の\((1,0)\)に向かって進む。すると,空港警察の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置①)。このとき,最適反応は\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。すると,乗客の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置②)。このとき,最適反応は\(p=0\)と\(q=1\)に切り替わるので,\((p,q)\)は左上隅の\((0,1)\)に向かって進む。すると,空港警察の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置③)。このとき,最適反応は\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。すると,乗客の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。そして,再び空港警察の最適反応のグラフ\(p=0.2\)にぶつかる(位置⑤)
以上のように,初期状態の向かう先は
\[\underbrace{ (1,0) → (1,1) → (0,1) → (0,0) }_{ ⓪→①→②→③→④ }→\underbrace{ (1,0) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると⑤の方がナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に収束する。
初期状態が\(\boldsymbol{(p^*+0.05,q^*-0.05)}\)の場合
初期状態(下図の位置⓪)における最適反応は\(p=1\)と\(q=1\)なので,\((p,q)\)は初期状態から右上隅の\((1,1)\)に向かって進む。すると,乗客の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置①)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は左上隅の\((1,0)\)に向かって進む。すると,空港警察の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置②)。このとき,最適反応は\(p=0\)と\(q=0\)に切り替わるので,\((p,q)\)は左下隅の\((0,0)\)に向かって進む。すると,乗客の最適反応のグラフ\(q=0.75\)を通り過ぎる(位置③)。このとき,最適反応は\(p=1\)と\(q=0\)に切り替わるので,\((p,q)\)は右下隅の\((1,0)\)に向かって進む。すると,空港警察の最適反応のグラフ\(p=0.2\)を通り過ぎる(位置④)。このとき,最適反応は再び\(p=1\)と\(q=1\)に切り替わるので,\((p,q)\)は右上隅の\((1,1)\)に向かって進む。そして,再び乗客の最適反応のグラフ\(q=0.75\)にぶつかる(位置⑤)。
以上のように,初期状態の向かう先は
\[\underbrace{ (1,1) → (0,1) → (0,0) → (1,0) }_{ ⓪→①→②→③→④ }→\underbrace{ (1,1) → ・・・ }_{ ⑤→・・・ }\]
と繰り返す。これによって,\((p,q)\)は初期状態(位置⓪)から螺旋状に動く。ここで,位置⓪と位置⑤を見比べると,⑤の方がナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に近付いている。従って螺旋状に動きながらナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に収束する。
(ウ)以上の議論をまとめると,どの領域からスタートしても最適反応動学は以下の二つを繰り返す。
- \(p=0.2\)にぶつかり,空港警察の最適反応が切り替わり,\(q\)の動く向きが逆になることで\(q=0.75\)に戻ってくる。
- \(q=0.75\)にぶつかり,乗客の最適反応が切り替わり,\(p\)の動く向きが逆になることで\(p=0.2\)に戻ってくる。
そして\((p,q)\)は螺旋を描いてナッシュ均衡\((p^*,q^* )=(0.2,0.75)\)に収束する。これは初期状態がどこにあったかに依らないので,ナッシュ均衡\(\boldsymbol{(p^*,q^* )=(0.2,0.75)}\)は大域的に安定であると言える。
問題4.2(歩くか止まるか)
(ア) 各\(q\)に対する止まる人の最適反応は以下のようになる。
- \(q \lt 0.2\)ならば止まる人は\(p=1\)のみが最適反応。
- \(q=0.2\)ならば止まる人は\(p\)が\(0\)から\(1\)のどれでも最適反応。
- \(q>0.2\)ならば止まる人は\(p=0\)のみが最適反応。
-
各\(p\)に対する歩く人の最適反応は以下のようになる。
- \(p \lt 0.4\)ならば歩く人は\(q=1\)のみが最適反応。
- \(p=0.4\)ならば歩く人は\(q\)が\(0\)から\(1\)のどれでも最適反応。
- \(p>0.4\)ならば歩く人は\(p=0\)のみが最適反応
-
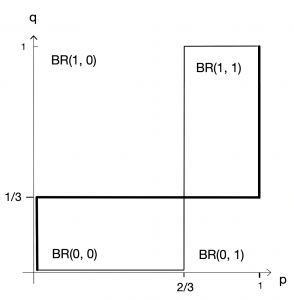
従って最適反応図は下図のようになる。太線が止まる人,細線が歩く人の最適反応である。
よってナッシュ均衡は\((p,q)=(1,0),(0.4,0.2),(1,0)\)の3つである。
(イ)ナッシュ均衡(1,0). 初期状態が\(p>0.4\)かつ\(q \lt 0.2\)の範囲,つまり\((0.4,0.2)\)の左上ならば,\((1,0)\)からどんな方向にずれていても,最適反応が\(p=0\)と\(q=1\)のまま,再び\((1,0)\)に収束する。従って,このナッシュ均衡\((1,0)\)は安定である。
ナッシュ均衡(0,1). 初期状態が\(p \lt 0.4\)かつ\(q>0.2\)の範囲,つまり\((0.4,0.2)\)の右下ならば,\((0,1)\)からどんな方向にずれていても,最適反応が\(p=1\)と\(q=0\)のまま,再び\((0,1)\)に収束する。従って,このナッシュ均衡\((0,1)\)は安定である。
ナッシュ均衡(0.4,0.2). 上で見たようにどんなに微少でも(0.4,0.2)から左上や右下にずれると,別のナッシュ均衡(1,0),あるいは\((0,1)\)に収束してしまう。従って,このナッシュ均衡(0.4,0.2)は不安定である。
東日本では「止まる人は左・歩く人は右」が定着しているが,西日本では逆に「止まる人は右・歩く人は左」が定着している。東日本の人が西日本に行った際に最初に降り立つ場所は,新大阪駅や京都駅などであり,これらの場所は西日本の中でも数日前まで東日本にいた人の割合が高い場所である。しかし,このような新大阪駅でさえも「止まる人は右・歩く人は左」が定着している。これは西日本の状態,つまりナッシュ均衡\((0,1)\),が局所的に安定であるからだと考えられる。新大阪駅のように,東日本の人が多少増えて\((p,q)\)が\((0,1)\)から右下に移動しようが,依然最適反応が\(p=0\)と\(q=1\)になっているので,再び「止まる人は右・歩く人は左」の状態に戻ってしまう。
問題4.3(ピグー税のアイディア)
通行料\(d\)があるので,常盤道を使うドライバーの割合を\(p\)としたとき,常盤道からの利得は\(10-d-8p\)となる。他方で国道からの利得は\(4+p\)のままである。
(ア) \(d=3\)の下での,ドライバーにとって常磐道と国道が無差別になる条件は
\[7-8p=4+p,つまり p=1/3\]
である。\(p=1\)(みんなが常磐道)なら国道が,\(p=0\)(みんなが国道)なら常磐道が各ドライバーの最適反応であることと合わせると,各\(p\)に対する最適反応は以下のようになる。
- \(p \lt 1/3\)ならば常盤道のみが最適反応。
- \(p=1/3\)ならば常盤道と国道どちらでも最適反応。
- \(p>1/3\)ならば国道のみが最適反応。
従って最適反応動学は以下のようになる。
- \(p \lt 1/3\)ならば\(p\)は増えていく。
- \(p=1/3\)ならば\(p\)は増えるとも減るとも変わらないともどちらでも言える。
- \(p>1/3\)ならば\(p\)は減っていく。
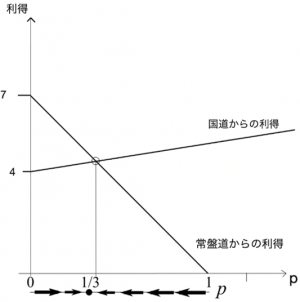
下図の上側は各戦略の利得,下側は最適反応動学を示す。
ナッシュ均衡は\(p=1/3\)である。またこの均衡は大域的に安定である。何故なら\(p^*=1/3\)からどちらの方向にどれだけズレたとしても,再び\(p^*=1/3\)に戻るからである。
答え:ナッシュ均衡は\(\boldsymbol{(p=1/3}\)。この均衡は大域的に安定である。
ナッシュ均衡が\(p=1/2\)になるように\(d\)を設定したい。\(p=1/2\)では国道を取るドライバーも常磐道をとるドライバーもいるので,それが均衡なら両方とも最適反応として同じ利得でないといけない。つまり,\(d\)は
\[10-d-8×\frac{1}{2}=4+\frac{1}{2}\]
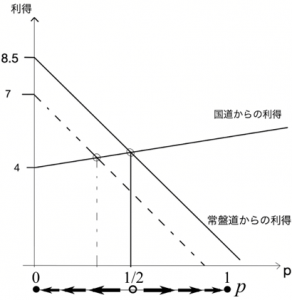
を満たさないといけない。これを解くと\(d=1.5\)を得る。下図の上側は\(d=1.5\)の下での利得,下側は最適反応動学を示す。(ア)と同様にこの均衡\(p=1/2\)は大域的に安定である。
答え:\(\boldsymbol{p^*=1/2}\)をナッシュ均衡にさせるのは\(\boldsymbol{d=1.5}\)。このときナッシュ均衡は大域的に安定。
追記)社会全体の利得の合計(総余剰)を求めよう。常磐道を通るドライバーは一人当たり\(10-d-8p\)の利得を得て,そうしたドライバーの割合が\(p\)なので,これらのドライバーの利得の合計は\((10-d-8p)p\)となる。これらのドライバーから集めた通行料\(dp\)も徴収する主体(国Sや道路の運営者)の収入としてカウントする。そして,国道を通るドライバーの利得の合計は\((4+p)(1-p)\)である。これらをすべて足し合わせると,
\[(10-d-8p)p+dp+(4+p)(1-p)=-9p^2+7p+4\]
である。これを偏微分するなり,2次関数なので平方完成させるなりすると,総余剰を最大にする\(p\)は\(p=7/18\)だとわかる。そして,これを均衡にするような\(d\)は
\[10-d-8×\frac{7}{18}=4+\frac{7}{18}\]
を満たさないといけない。これを解くと\(d=2.5\)を得る。