PDFファイル

【小俵将之・浅古泰史・森谷文利・図斎大】

• 問題3.1
• 問題3.2
• 問題3.3

問題3.1（今までのモデルの総復習）

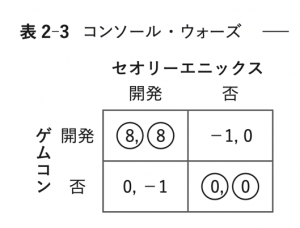
（ア）　コンソール・ウォーズ(表2-3)
Step 1.　それぞれのプレーヤーの最適反応を利得表に○で示す。

Step 2.　ゲムコンが開発を選ぶ確率を\(p\)，セオリーエニックス（セオエニ）が開発を選ぶ確率を\(q\)とする。ゲムコンにとって開発か否かが無差別になるのは

\[8q-(1-q)=0q+0(1-q)，つまり　q=1/9\]

のときである。同様にセオエニにとって開発か否かが無差別になるのは\(p=1/9\)のときである。

Step 3. 以上の結果に「極端な性質」を当てはめて，混合戦略でのそれぞれの最適反応がわかる。

• 各\(q\)に対するゲムコンの最適反応は以下のようになる。
  • \(q>1/9\)ならば，ゲムコンは\(p=1\)のみが最適反応。
  • \(q=1/9\)ならば，ゲムコンは\(p\)が\(0\)から\(1\)のどれでも最適反応。
  • \(q \lt 1/9\)ならば，ゲムコンは\(p=0\)のみが最適反応。
• 各\(p\)に対するセオエニの最適反応は以下のようになる。
  • \(p>1/9\)ならば，セオエニは\(q=1\)のみが最適反応。
  • \(p=1/9\)ならば，セオエニは\(q\)が\(0\)から\(1\)のどれでも最適反応。
  • \(p \lt 1/9\)ならば，セオエニは\(q=0\)のみが最適反応。

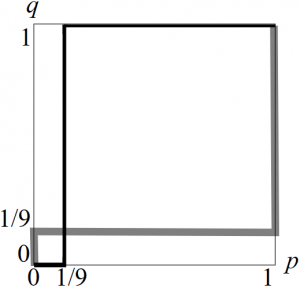
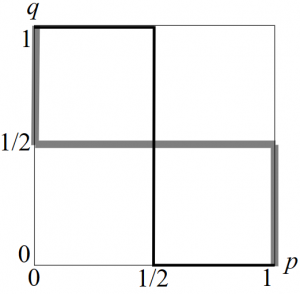
従って最適反応は以下のように図示できる。灰色の太線がゲムコン，黒色の細線がセオエニの最適反応である。

ナッシュ均衡は\(\boldsymbol{(p,q)=(0,0),(1,1),(1/9,1/9)}\)の3つである。特に，混合戦略均衡\((p,q)=(1/9,1/9)\)は，互いに\(1/9\)の確率で開発を選んでいる状況と解釈できる。新しいゲーム機への参入はゲームメーカーにとっては一回きりの大きな意思決定なので，ランダムな手を意図的に取るとは考えにくいだろう。また利得の構造から言っても，開発を選ぶならば，相手に手を読まれたくないというよりも，相手にもそれを正しく予見して共に開発したほうが利得が高くなる。従って，この解釈の下では混合戦略均衡\((p,q)=(1/9,1/9)\)が現実的に起きているとは考えにくい。（しかし，だからといってこの均衡を無視できるわけではなく，例えば第４章で学ぶ進化動学の下では，\((0,0),(1,1)\)のどちらに収束するかを決めるクリティカルマスとして鍵になる。）

（イ）　ATMの共同運用(表2-5)
Step 1.　それぞれのプレーヤーの最適反応を利得表に○で示す。
Step 2.　吉左衛門銀行がシステムKを選ぶ確率を\(p\),弥太郎銀行がシステムKを選ぶ確率を\(q\)とする。 吉左衛門銀行にとってシステムKとシステムYが無差別になるのは

\[90q-10(1-q)=-30q+70(1-q)，つまり　q=2/5\]

のときである。同様に弥太郎銀行にとってKとYが無差別になるのは\(p=3/5\)のときである。

Step 3.　以上の結果に「極端な性質」を当てはめて，混合戦略でのそれぞれの最適反応がわかる。

• 各\(q\)に対する吉左衛門銀行の最適反応は以下のようになる。
  • \(q>2/5\)ならば,吉左衛門銀行は\(p=1\)のみが最適反応。
  • \(q=2/5\)ならば,吉左衛門銀行は\(p\)が\(0\)から\(1\)のどれでも最適反応。
  • \(q \lt 2/5\)ならば,吉左衛門銀行は\(p=0\)のみが最適反応。
• 各\(p\)に対する弥太郎銀行の最適反応は以下のようになる。
  • \(p>3/5\)ならば,弥太郎銀行は\(q=1\)のみが最適反応。
  • \(p=3/5\)ならば,弥太郎銀行は\(q\)が\(0\)から\(1\)のどれでも最適反応。
  • \(p \lt 3/5\)ならば,弥太郎銀行は\(q=0\)のみが最適反応。

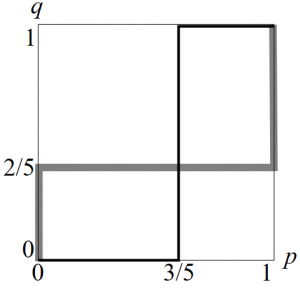
従って最適反応は以下のように図示できる。灰色の太線が吉左衛門銀行，黒色の細線が弥太郎銀行の最適反応である。

ナッシュ均衡は\(\boldsymbol{(p,q)=(0,0),(1,1),(3/5,2/5)}\)の3つである。特に，混合戦略均衡\((p,q)=(3/5,2/5)\)は，互いの銀行がランダムにシステムを選んでいる状況と解釈できる。(ア)のコンソール・ウォーズと同様に，銀行にとってシステムの選択は大きな決断であること，そして相手に手を読まれないようにすることの得がないことから，混合戦略均衡\((p,q)=(3/5,2/5)\)は現実的とは言い難い。

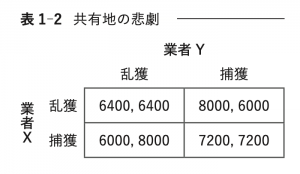
（ウ）　魚の乱獲問題(表1-2)
業者Xも業者Yも「乱獲」が強支配戦略になっている。従って，相手がどんな混合戦略を取っていたとしても，純戦略「乱獲」のみが最適反応になる。よって，ナッシュ均衡は(乱獲,乱獲)，つまり業者Xが乱獲を選ぶ確率を\(p\)，業者Yが乱獲を選ぶ確率を\(q\)とすると，\(\boldsymbol{(p,q)=(1,1)}\)のみである。

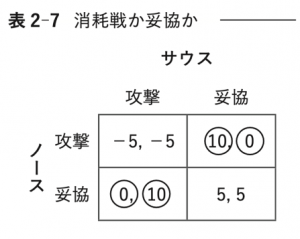
（エ）　消耗戦(表2-7)
Step 1.　それぞれのプレーヤーの最適反応を利得表に○で示す。

Step 2.　ノースが攻撃を選ぶ確率を\(p\),サウスが攻撃を選ぶ確率を\(q\)とする。ノースにとって攻撃と妥協が無差別になるのは

\[-5q+10(1-q)=0q+5(1-q)，つまり　q=1/2\]

のときである。同様にサウスにとって攻撃と妥協が無差別になるのは\(p=1/2\)のときである。

Step 3.　以上の結果に「極端な性質」を当てはめて，混合戦略でのそれぞれの最適反応がわかる。

• 各\(q\)に対するノースの最適反応は以下のようになる。
  • \(q \lt 1/2\)ならば,ノースは\(p=1\)のみが最適反応。
  • \(q=1/2\)ならば,ノースは\(p\)が\(0\)から\(1\)のどれでも最適反応。
  • \(q>1/2\)ならば,ノースは\(p=0\)のみが最適反応。
• 各\(p\)に対するサウスの最適反応は以下のようになる。
  • \(p \lt 1/2\)ならば,サウスは\(q=1\)のみが最適反応。
  • \(p=1/2\)ならば,サウスは\(q\)が\(0\)から\(1\)のどれでも最適反応。
  • \(p>1/2\)ならば,サウスは\(q=0\)のみが最適反応。

従って最適反応は以下のように図示できる。太線がノース，細線がサウスの最適反応である。

ナッシュ均衡は\(\boldsymbol{(p,q)=(0,1),(1,0),(1/2,1/2)}\)の3つである。混合戦略均衡\((p,q)=(1/2,1/2)\)は，互いに\(1/2\)の確率で攻撃と妥協をランダムに取っている状況と解釈できる。消耗戦では各国の軍が日々このような状況に面しており，また利得の構造から言っても相手に手を読まれたくない。なので，このようなランダムさを意図的に残す戦略も現実的だと言える。（ただし，やはり第４章の進化動学でこの均衡が安定的と言えるかはまた別のこと。）

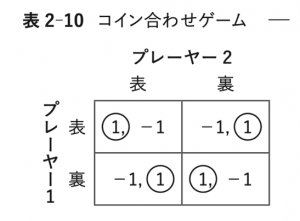
（オ）　コイン合わせゲーム(表2-10))
Step 1.　それぞれのプレーヤーの最適反応を利得表に○で示す。

Step 2.　プレーヤー1が表を選ぶ確率を\(p\),プレーヤー2が表を選ぶ確率を\(q\)とする。プレーヤー1にとって表と裏が無差別になるのは

\[1q-1(1-q)=-1q+1(1-q)，つまり　q=1/2\]

のときである。同様にプレーヤー2にとって表と裏が無差別になるのは\(p=1/2\)のときである。

Step 3.　以上の結果に「極端な性質」を当てはめて，混合戦略でのそれぞれの最適反応がわかる。

• 各\(q\)に対するプレーヤー1の最適反応は以下のようになる。
  • \(q>1/2\)ならば,プレーヤー1は\(p=1\)のみが最適反応。
  • \(q=1/2\)ならば,プレーヤー1は\(p\)が\(0\)から\(1\)のどれでも最適反応。
  • \(q \lt 1/2\)ならば,プレーヤー1は\(p=0\)のみが最適反応。
• 各\(p\)に対するプレーヤー2の最適反応は以下のようになる。
  • \(p \lt 1/2\)ならば,プレーヤー2は\(q=1\)のみが最適反応。
  • \(p=1/2\)ならば,プレーヤー2は\(q\)が\(0\)から\(1\)のどれでも最適反応。
  • \(p>1/2\)ならば,プレーヤー2は\(q=0\)のみが最適反応。

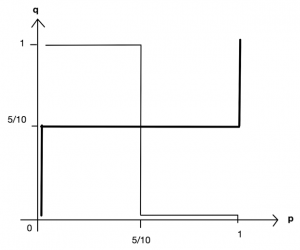
従って最適反応は以下のように図示できる。太線がプレーヤー1，細線がプレーヤー2の最適反応である。

ナッシュ均衡は\(\boldsymbol{(p,q)=(1/2,1/2)}\)のみである。混合戦略均衡\((p,q)=(1/2,1/2)\)は，互いに\(1/2\)の確率で表と裏をランダムに取っている状況と解釈できる。（エ）と同様に，コイン合わせは日常のものであり，また相手に手を読まれたくない状況なので，この混合戦略均衡\((p,q)=(1/2,1/2)\)は現実的だと言える。

問題3.2（厳しい罰を下す手荷物検査）

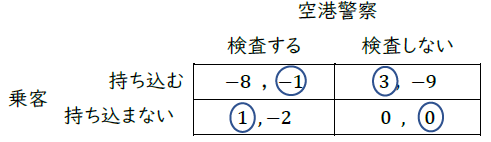
（ア）　このゲームの利得表は以下で与えられる。
Step 1.　それぞれのプレーヤーの最適反応を利得表に○で示す。

Step 2.　乗客が禁止物を持ち込む確率を\(p\),空港警察が検査をする確率を\(q\)とする。乗客にとって持ち込むのと持ち込まないのが無差別になるのは

\[-8q+3(1-q)=1q+0(1-q)，つまり　q=0.25\]

のときである。同様に空港警察にとって検査するのとしないのが無差別になる条件は\(p=0.2\)である。

Step 3. 　以上の結果に「極端な性質」を当てはめて，混合戦略でのそれぞれの最適反応がわかる。
このゲームのナッシュ均衡を求める。

• 各\(q\)に対する乗客の最適反応は以下のようになる。
  • \(q \lt 0.25\)ならば,乗客は\(p=1\)のみが最適反応。
  • \(q=0.25\)ならば,乗客は\(p\)が\(0\)から\(1\)のどれでも最適反応。
  • \(q>0.25\)ならば,乗客は\(p=0\)のみが最適反応。
• 各\(p\)に対する空港警察の最適反応は以下のようになる。
  • \(p>0.2\)ならば,空港警察は\(q=1\)のみが最適反応。
  • \(p=0\).2ならば,空港警察は\(q\)が\(0\)から\(1\)のどれでも最適反応。
  • \(p \lt 0.2\)ならば,空港警察は\(q=0\)のみが最適反応。

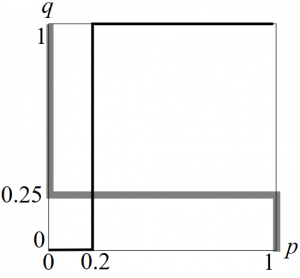
従って最適反応は以下のように図示できる。灰色の太線が乗客，黒色の細線が空港警察の最適反応である。ナッシュ均衡は\((p,q)=(0.2,0.25)\)のみである。

（イ）　表3.6のナッシュ均衡\((0.2,0.75)\)から，\((0.2,0.25)\)に均衡が変化した。つまり，危険物持ち込みの厳罰化によって乗客が危険物を持ち込む確率\(p\)は変わらず，空港警察が検査する確率\(q\)が下がった。

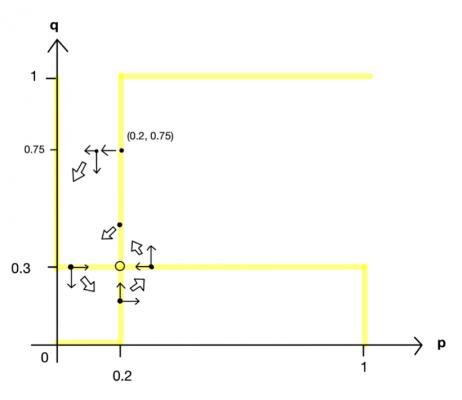
乗客の確率は変わらずに空港警察の確率が変わった理由として，下図のような螺旋型の移行過程が考えられる。

まず乗客・空港警察が\((p,q)=(0.2,0.75)\)を選んでいるときに，危険物持ち込みが厳罰化されたとする。このとき，検査確率\(q=0.75\)に対する乗客の最適反応は「持ち込まない」である。よって，厳罰を恐れる乗客は危険物持ち込みを控えるので，\(p\)は\(0.2\)から下がり始める。すると，危険物が持ち込まれる確率が\(0.2\)より下がったので，空港警察の最適反応は「検査しない」になる。よって，検査する確率\(q\)も\(0.75\)から下がり始める。以上より，\((p,q)=(0.2,0.75)\)から左下に徐々に移行する。

検査する確率\(q\)が\(0.25\)を下回ったとき，「持ち込む」が乗客の最適反応になるので\(p\)は再び上昇する。一方，\(p \lt 0.2\)である限り「検査しない」が空港警察の最適反応なので\(q\)は下がり続ける。以上より\(q=0.25\)まで下がったタイミングで\((p,q)\)は右下に移行し始める。

持ち込む確率\(p\)が\(0.2\)を超えたとき，空港警察は「検査する」が最適反応になるので検査する確率\(q\)は再び上昇する。一方，\(q \lt 0.25\)である限り乗客の最適反応は「持ち込む」なので\(p\)は上昇し続ける。以上より\(p\)が\(0.2\)まで上がったタイミングで\((p,q)\)は右上に移行し始める。

検査する確率\(q\)が\(0.25\)を超えたとき，乗客は「持ち込まない」が最適反応になるので\(p\)は再び減少する。一方，\(p>0.2\)である限り検査確率\(q\)は上がり続ける。以上より，\(q=0.25\)まで上がったタイミングで\((p,q)\)は左上に移行し始める。

以上のように\((p,q)\)は\((0.2,0.25)\)の周りを螺旋状に移動しながら，いずれ\((p,q)=(0.2,0.25)\)の均衡に落ち着く。以上の過程が落ち着くときには，乗客が危険物を持ち込む確率\(p\)は変化前の均衡\((0.2,0.75)\)から変わらず，空港警察が検査する確率\(q\)が下がっている。

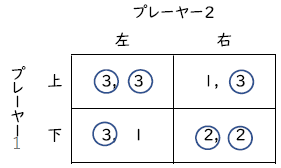
問題3.3（均衡選択のアイデア）

それぞれのプレーヤーの最適反応を利得表に○で示す。これから，（上，左）と（下，右）の二つがナッシュ均衡だとわかる。

弱支配基準

1. プレーヤー1にとって上は下に弱支配されている。なぜなら，プレーヤー2が左を取る時には共に利得3を与えるものの，右を取る時には下からの利得が２で上からの利得１よりも高くなるからである。（同様にプレーヤー２にとって左は右に弱支配されている。従って，弱支配基準に従うと，（上，左）は棄却され，（下，右）のみ残る。
2. 例：「上/左」を「親切」，「下/右」を「不親切」と読み換えると，このゲームは本文モデル3.3の大都会のゲームと同じ利得の構造（戦略の組の間の大小関係）を持っているとわかるので，このモデルで考えよう。「親切」にすると，相手にとっては（その他者自身の選択に寄らず）良くするものの，相手も同じく「親切」にしてくれていない限りは自らは（不親切にするのと比べても）損してしまう。他方で，不親切にするのは，均衡ではパレート最適ではないものの，相手の選択に寄らず，親切にするよりかは自分自身は損せず，無難ではある。この大都会では，いろんな人とのそのときどきの匿名的な体験の中でどんな行動を取っていくのかを学んでいくであろう。そうすると，自分が親切にしていても，不親切な相手とも出会い傷つき，そして自らも無難に不親切になっていくだろうから，弱支配基準が当てはまりやすいと言える。

利得支配基準

1. （上，左）はパレート最適であるが，（下，右）はそうでない。前者に関してはこの均衡で各プレーヤーが得ている利得３というのが，このゲームでのすべて戦略の組で達成しうる中で最も高い利得なので，ここからどう戦略を変えようが利得がこれ以上高くないからである。後者については（下，右）から（上，左）に二人のプレーヤーが一緒に変えることで，それぞれの利得が２から３に上がるからである。（ちなみにパレート最適でないことをいうには，他のプレーヤーの利得を下げずに，誰か少なくとも一人の利得を上げられることを示せれば十分である。）
2. 例：やはり「親切・不親切」の選択で考えてみよう。大都会ではなく，お互いに隣近所を（良くも悪くも）知っていて密に話をする，小さな村落を想定しよう。（あるいは都市部でも少子化の地域の子ども会を考えてもよかろう。）に，そうしたところでは，祭りや葬式の手伝い，用水路の掃除など，住人同士が一緒に労力を出すことがある。ここで「親切」として誰かが積極的に労力供給できるなら祭り等は成功する。自分一人だけ労力を供給するのなら，しんどさが残るが，みなが加わるなら打ち上げの飲み会や茶飲みで労力も報われよう。他方で，誰も「不親切」で消極的なら，そもそも祭り等はつぶれてしまう。しかし，こうした小さなグループでなら，そもそもの準備のうちから，日常的にお互いに手伝うかどうかを話し合いを重ねていくだろう。そのような会話を重ねるうちに，どのような選択を各々がするべきかを調整していくものだとすると，利得支配基準が当てはめられる。