3戦略の混合戦略

PDFファイル

【図斎　大】

１. すべての選択肢を混ぜる均衡

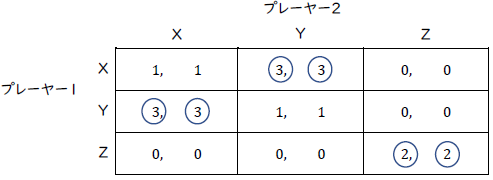
ここでは以下のようなゲームを考えましょう。

例によって丸で各プレーヤーの最適反応を示しています。それでわかるように，このゲームにはいろいろなナッシュ均衡があります。二人ともZを取る(Z,Z)，互い違いにXとYを取る(X,Y), (Y,X)が純粋戦略の均衡で見つかりますね。となると，混合戦略の均衡もあるでしょう。

その中でもまずはすべての選択肢X,Y,Zを混ぜるような均衡を求めてみましょう。ナッシュ均衡でどの選択肢も使うということは，どの選択肢も等しい期待利得を与えていて無差別になるということです。従って，まずは選択肢X,Y,Zをプレーヤー２が取る確率をそれぞれ\(x_2,y_2,z_2\)として，プレーヤー１にとっての各選択肢の期待利得を書き下してみましょう。

選択肢Xの期待利得：\(x_2+3y_2\)
選択肢Yの期待利得：\(3x_2+y_2\)
選択肢Zの期待利得：\(2z_2\)

これらが全て等しいということは

\[x_2+3y_2=3x_2+y_2=2z_2\]

が成り立つということです。またすべての選択肢の確率を足し合わせると１にならないといけないのですから，\(x_2+y_2+z_2=1\)も成り立たないといけません。従って，３本の等式の連立方程式

\[
\begin{eqnarray}
\left\{
\begin{array}{l}
x_2+3y_2=3x_2+y_2, \\
3x_2+y_2=2z_2, \\
x_2+y_2+z_2=1
\end{array}
\right.
\end{eqnarray}
\]

が成り立たないといけません。この連立方程式を解くと

\[(x_2,y_2,z_2 )=(0.25,0.25,0.5)\]

としてプレーヤー２の均衡戦略が求められます。同様に，プレーヤー２の無差別条件からプレーヤー１の均衡戦略が求められるでしょう。そこで選択肢X, Y, Zをプレーヤー１が取る確率をそれぞれ\(x_1,y_1,z_1\)とすると，プレーヤー１にとって各選択肢の期待利得が等しくなるということは

\[x_1+3y_1=3x_1+y_1=2z_1\]

が成立することです。実際プレーヤー１とプレーヤー２の利得は対称的なので，添え字になっているプレーヤー名の1を2に変えると，先のプレーヤー２にとっての無差別条件と同じになりますね。従ってx_1+y_1+z_1=1とともに，このプレーヤー２の無差別条件を解くと，先と同様に

\[(x_1,y_1,z_1 )=(0.25,0.25,0.5)\]

としてプレーヤー１の均衡戦略が求められます。以上で，まずプレーヤー１がプレーヤー１もプレーヤー２も共に\((x_1,y_1,z_1 )=(x_2,y_2,z_2 )=(0.25,0.25,0.5)\)という混合戦略を使い，両者ともにすべての選択肢を混ぜるナッシュ均衡が求められました。

２. 使わない選択肢がある均衡

利得表をよく見ると，選択肢Zを相手が使ってないのなら，選択肢X,Yが互い違いに最適反応になって，また選択肢Zはどうやらどちらよりも利得が高くなることはなさそうですね。なので，選択肢X,Yだけ混ぜて，選択肢Zを使わないという戦略も均衡になりそうです。そのように，使わない選択肢がある均衡では，単に使う選択肢どうしの無差別条件だけでなくて，使っていない選択肢が使っている選択肢よりも利得が高くなっていないことも確認しないといけません。

それをまずプレーヤー１の利得からやってみましょう。プレーヤー１が選択肢X,Yを使うのなら，両者は無差別になるので

\[x_2+3y_2=3x_2+y_2\]

という等式が成り立たないといけません。他方でプレーヤー2も選択肢Zを使わないのですから，\(z_2=0\)であり，プレーヤー２は選択肢X，Yに全確率１を割り振る，つまり\(x_2+y_2=1\)が成り立つはずです。以上の方程式を解くと，

\[(x_2,y_2,z_2 )=(0.5,0.5,0)\]

を得ます。同様に，プレーヤー２にとっての選択肢X,Yの間の無差別条件と，プレーヤー１もX,Yに確率１を割り振ることから，

\[(x_1,y_1,z_1 )=(0.5,0.5,0)\]

が成り立ちます。

以上で，均衡戦略がもうわかってしまいましたね。しかしこれでおしまいではなく，ちゃんと各プレーヤーについて，使っていない選択肢Zが本当に使わなくてもよかった，つまり利得が選択肢Ｘ，Ｙよりも良いわけではないことを示さないといけません。それは単に，上で特定された均衡戦略に基づいて，選択肢Zと選択肢X,Yの期待利得を計算して前者が後者よりは高くないことを示すだけです。\((x_2,y_2,z_2 )=(0.5,0.5,0)\)の下で，プレーヤー１にとって各選択肢の期待利得は

選択肢Xの期待利得：\(x_2+3y_2=2\)
選択肢Yの期待利得：\(3x_2+y_2=2\)
選択肢Zの期待利得：\(2z_2=0\)

であり，確かに選択肢Zは最適ではないと確認できました。従って，選択肢Zに確率ゼロを割り振る\((x_2,y_2,z_2 )=(0.5,0.5,0)\)というのが均衡戦略だとわかりました。同様にプレーヤー２にとっては

選択肢Xの期待利得：\(x_1+3y_1=2\)
選択肢Yの期待利得：\(3x_1+y_1=2\)
選択肢Zの期待利得：\(2z_1=0\)

なので，選択肢Zは最適ではなく，それに確率ゼロを割り振る\((x_2,y_2,z_2 )=(0.5,0.5,0)\)というのが均衡戦略だとわかりました。

以上をまとめると，戦略の数が２だけではないときの混合戦略のナッシュ均衡は以下のように求められます。

(1) まず，正の確率を割り振って，使う選択肢どうしの無差別条件から，相手の均衡戦略を特定する。これを各プレーヤーについてまずやりきる。
(2) そしてその特定した均衡戦略の下での，各選択肢の期待利得を計算する。そして，使っていない，ゼロの確率を割り振る選択肢が，使う選択肢よりも期待利得が高くはならないことを確認する。

ちなみにＸを使わずに，Ｙ，Ｚを混ぜるのは均衡になるでしょうか？まずプレーヤー１の利得からやってみましょう。選択肢Y,Zが使われるのなら，両者は無差別になるので

\[3x_2+y_2=2z_2\]

という等式が成り立たないといけません。また選択肢Xを使わないのですから，\(x_2=0\)であり，プレーヤー２は選択肢X，Yに全確率１を割り振る，つまり\(y_2+z_2=1\)が成り立つはずです。以上の方程式を解くと，

\[(x_2,y_2,z_2 )=(0,2/3,1/3)\]

を得ます。利得が対称的であるプレーヤー２についても，選択肢Ｙ, Zの間の無差別条件と，Y, Zにプレーヤー2は確率１を割り振ることから，

\[(x_1,y_1,z_1 )=(0,2/3,1/3)\]

が成り立ちます。\((x_2,y_2,z_2 )=(0,2/3,1/3)\)の下でプレーヤー１にとっては

選択肢Xの期待利得：\(x_2+3y_2=2\)
選択肢Yの期待利得：\(3x_2+y_2=2/3\)
選択肢Zの期待利得：\(2z_2=2/3\)

となり，使われないはずの選択肢Xこそが最適だということになりました。同様にしてプレーヤー１に関しても使われないはずの選択肢Xこそが最適だとわかります。従ってXを使わずに，Y，Ｚを混ぜるような均衡はありません。また，Ｙを使わずに，Ｘ，Ｚを混ぜるような均衡がないことも同様に示せます。これは練習として試してみてください。（同じような計算になります。）またオンライン・コンテンツ4.2では，同じ例を引き続き検討し，最適反応を図示して最適反応動学を考えています。

練習問題（ジャンケンゲーム）　
序章の事例0.1で紹介した権太と権助のジャンケンゲームを考える。権太がグー，チョキ，パーそれぞれを出す確率を\(x_1,y_1,z_1\)と，権助がグー，チョキ，パーそれぞれを出す確率を\(x_2,y_2,z_2\)とおこう。

（ア）モデル0.1のジャンケンゲームの標準形を，利得表を用いて示せ。このゲームのナッシュ均衡は実体験から予想されるように，「グー，チョキ，パーをそれぞれ等確率で選ぶ」である。二人とも等確率の混合戦略（\(1/3\)ずつの確率で，それぞれの純粋戦略を選ぶこと）を取ることが均衡であることを証明せよ。

（イ）権太（プレーヤー１）はバレーボールで人差し指を骨折するほどひどく突き指した。そのために今は人差し指にギブスをまいており縮められない。つまり，グーを出せない。このことを踏まえて，(ア)で示した利得表を修正し，そして混合戦略の選択を許容した際のナッシュ均衡を求めよ。

ヒント：権太の取りうる戦略はチョキとパーのみであるため，権助は強く支配される戦略を有している。

（ウ）（イ）の均衡下での両プレーヤーの期待利得も計算せよ。権太のみならず権助の利得も（ア）とは変わるはずだが，どのように変わり，そしてなぜそのように変わるか説明せよ。

ヒント：説明に当たっては，権助が負けることがあるのかを考えてみよう。

（エ）権太の突き指は治る，今はギブスをまいていない。よって，グーも出せるが，それでも少しは痛む。どれくらいの痛みかというと，餃子1/2個を食べることの至福を打ち消すほどである。つまり，利得が4減るくらいの苦痛である。もちろんグーを出したにもかかわらず，餃子が食べられない場合には，この苦痛しか残らない。このことを踏まえて，(ア) で示した利得表を修正し，そして混合戦略の選択を許容した際のナッシュ均衡を求めよ。　

解答

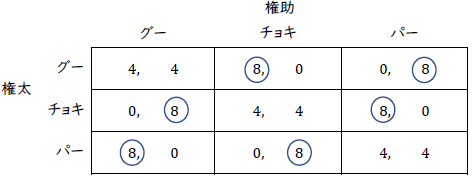
（ア）相手が等確率で３つの手を出すのなら，自分が出せるそれぞれの手（純粋戦略）では確率\(1/3\)で勝って利得8を，確率\(1/3\)で引き分けて利得\(4\)を，確率\(1/3\)で負けて利得\(0\)を得る。従ってどの手でも期待利得は\(8/3+4/3+0/3=4\)となり等しい。なので自らも等確率で３つの手を出すのは最適反応になっている。これが権太，権助のそれぞれで言えるので，二人それぞれが確率\(1/3\)ずつで３つの手を出すのはナッシュ均衡になっている。

（イ）権助にとってパーはチョキに強く支配されているので，ナッシュ均衡でパーを出すことはない。なので，太線で囲った部分だけを注目すればよい。これは第３章の本文で解いたような２戦略のゲームなので同様に解くと，権太は「チョキを確率\(2/3\)で，パーを確率\(1/3\)で出す」という戦略，権助は「グーを確率\(1/3\)で，チョキを確率\(2/3\)で出す」という戦略がナッシュ均衡とわかる。実際，このときの権助のそれぞれの手の期待利得は，

グー：　\(2/3⋅8+1/3⋅0=16/3\)
チョキ：\(2/3⋅4+1/3⋅8=16/3\)
パー：　\(2/3⋅0+1/3⋅4=4/3\)

でパーはグー，チョキに比べると低い。

（ウ）権太の期待利得は

\[2/3 (1/3⋅0+2/3⋅4)+1/3 (1/3⋅8+2/3⋅0)=2/3⋅8/3+1/3⋅8/3=8/3, \]

権助の期待利得は

\[1/3 (2/3⋅8+1/3⋅0)+2/3 (2/3⋅4+1/3⋅8)=1/3⋅16/3+2/3⋅16/3=16/3\]

である。やはり権太の利得は低くなり，権助の利得は高くなっている。まず権太がグーを出せなくなったので権助はパーを出しさえしなければ，権太がチョキを出したときに悪くてもあいこになって負けることがなくなった.なので権太はチョキをもっと（確率\(2/3\)）出しやすくなり，それでせめてあいこにするために権助もチョキをもっと（確率\(2/3\)）出すようになった.そのおかげで権助はグーを出した時にももっと勝ちやすくなった。

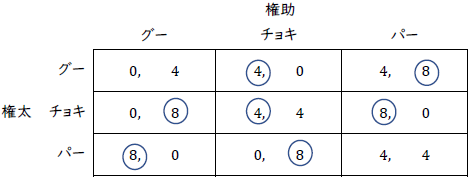
（エ）権助の戦略\((x_2,y_2,z_2 )\)の下で，権太の３つの手それぞれからの期待利得は

グー：　\(0x_2+4y_2+4z_2\)
チョキ：\(0x_2+4y_2+8z_2\)
パー：　\(8x_2+0y_2+4z_2\)

となる。グーは\(z_2=0\)のときに限ってチョキと等しい利得を与え，もしも\(z_2>0\)ならチョキよりも利得は低くなるので最適となることはない。

これを基に，まずは権太が３つの手全てを取る均衡があるかを検討する。もしも権太がすべての手を取るならどれも無差別となり，また\(z_2=0\)でないといけないので

\[0x_2+4y_2=0x_2+4y_2=8x_2+0y_2\]

が成立する。これと\(x_2+y_2+z_2=1\)を連立させて解くと，

\[(x_2,y_2,z_2 )=(1/3,2/3,0)\]

を得る。他方で，権助はグーとチョキだけを取るので，この二つの手で無差別になるので，

\[4x_1+8y_1+0z_1=0x_1+4y_1+8z_1\]

が成り立つ。これと\(x_1+y_1+z_1=1\)を連立させても２本しか方程式がないので，\((x_1,y_1,z_1 )\)が一つには決まらない。ただ，\(z_1=1/3，x_1+y_1=2/3\)は満たさないといけない。権助にとってパーが（グーや）チョキよりも利得が高くなってはいけないので，\(z_1=1/3\)の下では

\[0x_1+4y_1+8⋅1/3≥8x_1+0y_1+4⋅1/3,　つまり　y_1≥2x_1-1/3\]

が成り立たないといけない。これと\(x_1+y_1=2/3\)を合わせると，\(x_1≤1/3\)を得る。つまり，権太の戦略は

\[(x_1,y_1,z_1 )=(x_1,2/3-x_1,1/3)，　但し　x_1≤1/3\]

を満たすものはどれでも，権助の戦略\((x_2,y_2,z_2 )=(1/3,2/3,0)\)とともにナッシュ均衡を成す。

では，\(z_2>0\)となる均衡があるかを検討する。このときには権太はグーが最適になることはないのでx_1=0となる。そのもとで権助の３つの手の期待利得は

グー：　\(8y_1+0z_1\)
チョキ：\(4y_1+8z_1\)
パー：　\(0y_1+4z_1\)

と表される。ここで\((y_1,z_1 )\)がどのようであっても，どちらかが正である限りは，\(4y_1+8z_1>0y_1+4z_1\)なのでパーが最適となることはない。従って権助はパーを取ることはなく，\(z_2>0\)と矛盾する。従って，\(z_2>0\)となる均衡はないと結論される。