共有地の悲劇のモデル
【浅古泰史】
本著第1章第3節の共有地の悲劇のモデルを思い出してみましょう。ある漁場で2つの水産業者AとBが魚を獲っています。漁船1艘あたりが獲ることができる魚の量は,その漁場に出る漁船の数に依存しています。業者Aが\(b_A\)艘の漁船を,そして業者Bが\(b_B\)艘の漁船を出した場合,1艘あたり
\[300-(b_A+b_B )トン\]
の魚が獲れると考えましょう。この設定から,1艘あたりの漁獲高に漁船の数をかけた\([300-(b_A+b_B )]×b_A\)トンが業者Aの漁獲総量になることがわかります。業者Bの漁獲総量は \([300-(b_A+b_B )]×b_B\)トンです。
1トンの魚は1万円で売れるとします。ですので,漁獲総量に1万円を掛けた値が,各業者の売上高になります。また,漁船1艘を運用するの費用として60万円の費用がかかるとします。よって,業者Aの売上高から費用を引いた利潤は
\[[300-(b_A+b_B )]×b_A-60b_A 万円\]
ということになります。業者Bの利潤は\([300-(b_A+b_B )]×b_B-60b_B\)万円です。
モデル1.1では,業者が有する選択肢は80艘(乱獲)か60艘(捕獲)であると考えていました。しかし実際には,いかなる値も選べると考えるべきでしょう。そこで,業者AとBは,それぞれ漁船の数として\(b_A\)と\(b_B\)の値をそれぞれ選択するとします。漁船の数は0以上のいかなる値でも良いとしましょう(\(b_A>0かつb_B>0\))。「どんな数でも選べる」とした場合には,その数を連続した変数として分析することが一般的です。漁船の数が12.25艘(\(b_A=12.25\))など小数点の値を取ることはない,と思われるかもしれませんが,計算を楽にするための単純化だと思ってください。
業者Aは利潤である\([300-(b_A+b_B )]×b_A-60b_A\)を最大化する\(b_A\)を選択するため,以下の最大化問題を解くことになります。
\[{\rm max}_{b_A} [300-(b_A+b_B )]×b_A-60b_A\]
これは書き換えると,
\[{\rm max}_{b_A} 300b_A-b_A^2-b_A b_B-60b_A\]
となり,もう一歩書き換えると,
\[{\rm max}_{b_A} 240b_A-b_A^2-b_A b_B\]
になります。この式を\(b_A\)で微分したうえで,それがゼロとなることが最大化の条件である一階の条件になります。よって,一階の条件は,
\[240-2b_A-b_B=0\]
です。二階微分すると-2となるので,この条件が最大化の条件であることがわかります。この一階の条件を書き直すと,以下の式になります。
\[b_A (b_B )=\frac{240-b_B}{2} \tag{1}\]
\(b_A (b_B )\)は,相手のプレーヤーの選択である\(b_B\)の値によって,業者Aにとっての最適な\(b_A\)がどのように変化するのかを示す関数になっています。よって,これが業者Aの最適反応を示す関数です。同様の計算から,業者Bの最適反応関数も以下のように求めることができます。
\[b_B (b_A )=\frac{240-b_A}{2} \tag{2}\]
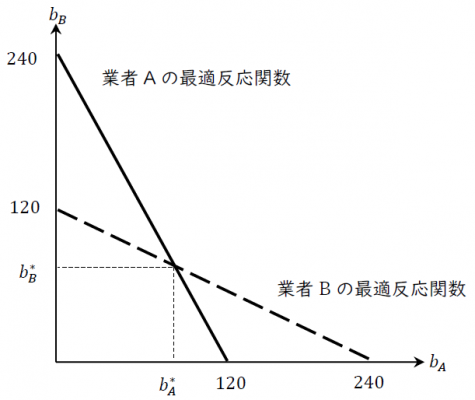
この2つの最適反応関数を図に書くと以下のようになります。実線が業者Aの最適反応関数であり,点線が業者Bの最適反応関数です。相手の漁船数が多いほど,1艘あたりの漁獲高を確保するために,控えめに漁船数を少なくしていきます。一方で,相手があまり漁船を出さない場合には,強気に漁船数を高めています。
ナッシュ均衡とは,プレーヤーがお互いに最適反応を選択している状態のことでしたね。つまり,上記の図では,両者とも最適反応関数の線上になるような漁船数を選択することになります。両者とも線上に乗るためには,2つの線の交点である必要があります。つまり,ナッシュ均衡は,上記の(1)と(2)の最適反応関数の連立方程式を解いた解であるということがわかります。図の中の\(b_A^*\)と右上に*がついている変数は,ナッシュ均衡における\(b_A\)の値を示しています。均衡の値を表すために,*をつけることはよく行われています。\(b_B^*\)も同様に,均衡上の値を意味します。それでは,解を求めるために,まずは式(2)を式(1)に代入して計算していきましょう。
\[b_A^*=\frac{240-\frac{240-b_A^*}2}2\]
これを少し計算してみると,
\[b_A^*=\frac{\frac{480-240+b_A^*}2}2\]
になります。さらにもう一歩進めると,
\[b_A^*=\frac{240}4+\frac{b_A^*}4\]
になり,さらにさらにもう一歩進めると,
\[\frac{3}4 b_A^*=60\]
になりますね。以上の計算の結果,ナッシュ均衡において業者Aが選択する漁船数が,以下のように算出されます。
\[b_A^*=80\]
この値を,式(2)に代入すると,ナッシュ均衡において業者Bが選択する漁船数も算出できます。
\[b_B^*=80\]
よって,「両業者共に80艘を選択する」ことがナッシュ均衡であることがわかります。第1章で,業者が選択できる1つの選択肢は,80艘を選択する「乱獲」であるとしました。これは,連続変数を考えた場合のナッシュ均衡の値だったことになります。ここまでの重要な点を,復習しておきましょう。
ここがポイント!
連続変数の選択に関して分析をする場合,
(1) 利得最大化問題を解いた一階の条件を変形して,最適反応関数を求められる。
(2) 全プレーヤーの最適反応関数を連立法的式として計算して得られた解が,ナッシュ均衡である。
それでは,このナッシュ均衡はパレート最適な結果なのでしょうか?そこで,両業者が協力した場合に,各業者の利潤を最大化するような漁船数は何か,計算してみましょう。そのためには,自分の漁船の数だけでなく,相手の数も同時に決定できると考える必要があります。第三者がいて,その第三者が両業者にとって好ましい漁船数を計算してあげているような状況です。そこで,\(b_A=b_B=b\)とおいて,利潤を最大化するような\(b\)の決定を分析します。総利潤は\([300-2b]×b-60b\),となりますので,最大化問題は以下の通りです。
\[{\rm max}_{b} [300-2b]×b-60b\]
書き換えると
\[{\rm max}_{b} 240-2b^2\]
になります。一階の条件は以下の通りです。
\[240-4b=0\]
これを計算し直すと,強調した場合に利潤を最大化するような漁船の数が求められます。
\[b^*=60\]
つまり,両業者がともに60艘を選択した方が,ともに80艘を選択するよりも,より高い利潤が得られることがわかります。現に,80艘の場合の利潤は,
\[\begin{align}
&240b_A-b_A^2-b_A b_B \\
&=240×80-80×80-80×80 \\
&=6400
\end{align}\]
であり,60艘の場合は
\[240×60-60×60-60×60=7200\]
になっています。これらの利潤の値も,本著の図1.2で用いていました。よって,80艘を選択するナッシュ均衡はパレート最適ではなく,囚人のジレンマと言える状況が生じていることがあります。式(1)より,相手が60艘を選んでいる場合(\(b_B=60\)),それへの最適反応は90艘(\(b_A (b_B )=90\))です。よって,ともに60艘を選択することは均衡にはなりません。
以上では,第2章で議論したナッシュ均衡に関して検討してきました。それでは,第1章の支配戦略の話を,このような連続変数を選択する場合に適応できるのでしょうか。業者Aの最適反応は式(1)に示してありますが,\(b_B=0\)のとき,\(b_A (b_B)=120\)であり,\(b_B\)が増えるごとに,業者Aの最適な漁船の数は減少しています。このことから,以下のことが言えます。
業者Aは120艘を超える漁船の数を絶対に選ばない。
言い換えると,120艘を超える漁船の数を出すことの利潤は,相手の漁船の数によらず,常に120艘ちょうどを出した時の利潤を下回ることになります。つまり,120艘を超える漁船数は,120艘という選択に支配をされている強く支配される戦略です。そこで,支配される戦略の逐次消去にならって,消去してしまいましょう。
120艘を超える漁船数を消去すると,相手が選択する漁船数として,ありえる最大の数は120艘です。これを最適反応関数である式(1)に代入すると,
\[b_A (120)=\frac{240-120}2=60\]
になります。つまり,相手が120艘を選択していれば,60艘が最適反応です。そして,相手の漁船数が120より少なくなると,最適な漁船数は増えていきます。よって,以下のことが言えます。
60艘未満の漁船数は絶対に選ばない。
言い換えると,60艘を下回る漁船の数を出すことの利潤は,相手の漁船の数によらず,常に60艘ちょうどを出した時の利潤を下回ります。つまり,60を下回る漁船数は強く支配される戦略なので,消去しちゃいます。
60艘未満の漁船数を消去すると,相手が選択する漁船数として,ありえる最小の数は60艘です。これを最適反応関数に代入すると,
\[b_A (60)=\frac{240-60}2=90\]
そして,相手の漁船数が60より多くなると,最適な漁船数は減っていきます。よって,90艘を超える漁船の数は強く支配される戦略となるので,消去できます。ちなみに,4.2項で議論した110艘(大乱獲)という選択肢はこの段階で消えますね。この後,同じことを繰り返していきます。
- 90艘を超える数を消した後では,75艘を下回る漁船数が強く支配される戦略なので消去します。この時点で60艘が消えます。
- 75艘未満を消した後では,82.5艘を超える漁船数が強く支配される戦略なので,消去します。
- 82.5艘を超える数を消した後は,78.75艘未満の漁船数が強く支配される戦略なので,消去します。
- 79.75艘未満を消した後は,80.75艘を超える漁船数が強く支配される戦略なので,消去します。
- 80.75艘を超える数を消した後は,79.625艘未満の漁船数が強く支配される戦略で,消去します。
と,この時点で整数の数しか選べないとすると,80艘が残されていることになります。また,整数に限らないとしても,この作業を(無限に)繰り返していくうちに,80艘ちょうどの漁船数であるケース以外は消されていきます。よって,このモデルでは,支配される戦略の逐次消去で生き残った戦略とナッシュ均衡の戦略が同一になるということがわかります。