3戦略の最適反応動学

PDFファイル

【図斎　大】

1. 3戦略の最適反応

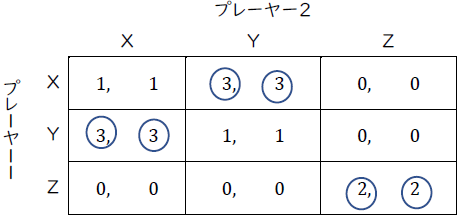
オンライン・コンテンツ3.2で考えた下のゲームを引き続きここでも考えます。ただ最適反応動学を図で考えるときに変数が多くなりすぎては，この2次元の紙の上では動学を描画できなくなりますね。なので，ここでは本文のモデル4.2のようなひとつの集団のポピュレーションゲームとしてとらえます。つまり，その集団の個々人は，別の個人と下の利得表で表されたゲームをプレーし利得を得るものとし，相手は集団全体から一様にランダムに選ばれるものだと仮定します。集団の中でX,Y,Zを取る人の割合をそれぞれ\((x,y,z)\)という確率分布で表すと，各個人はこの確率分布に基づいてX,Y,Zそれぞれの期待利得を計算したうえで，X,Y,Zのどれを選ぶかを決めるものだとします。

最適反応動学のためには，最初に最適反応を求めないといけないですね。この手順は第3章と同じです。まずは純粋戦略に対する最適反応を上の表で○をつけたように見つけます。そして，次は最適反応の境目を求めるのでしたね。そのために各選択肢の期待利得を書き下してみましょう。

選択肢Xの期待利得：\(x_2+3y_2\)
選択肢Yの期待利得：\(3x_2+y_2\)
選択肢Zの期待利得：\(2z_2\)

いきなりそれぞれが最適，つまり3つの中で一番高い利得を与えるような条件は求めにくいです。なので，代わりにX-Y, Y-Z, Z-Xのように2つで一組にして，組ごとに期待利得が等しくなる条件を見つけましょう。以下では\(x+y+z=1\)，つまり\(z=1-x-y\)であることを利用します。

XとY：\(x+3y=3x+y\)，つまり\(x=y\),
YとZ：\(3x+y=2z\)，つまり\(5x+3y=2\),
ZとX：\(2z=x+3y\)，つまり\(3x+5y=2\),

となります。

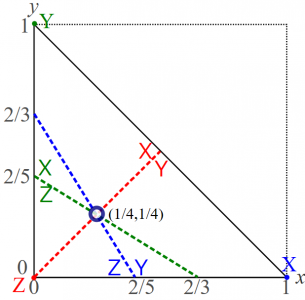
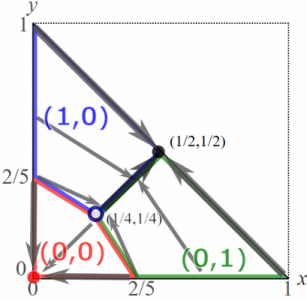
これを図示していくのですが，\((x,y,z)\)のままだと3次元が必要そうでしたが，\(z=1-x-y\)を使って\((x,y)\)だけにしたので2次元のグラフにできますね。以上3本の式をそれぞれ\((x,y)\)の座標でグラフにしましょう。下の図で，もちろん\((x,y)=(1,0)\)はXだけを取る純粋戦略，\((x,y)=(0,1)\)はYだけを取る純粋戦略を表しています。そして，原点\((x,y)=(0,0)\)はXもYも取る確率はゼロで，Zを取る確率は\(z=1-x-y=1-0-0=1\)なのでZだけを取る純粋戦略を表しています。原点から遠くなるほどZを取る確率が小さくなり，そして\((1,0)\)と\((0,1)\)を通る線上では\(x+y=1\)なので\(z=1-x-y=0\)でありZを取る確率がゼロになります。このようにこの原点，\((1,0), (0,1)\)を頂点とする三角形の中の点それぞれについて，\(x\)座標，\(y\)座標からX,Yを取る確率（割合）\(x,y\)が，それから\(z=1-x-y\)を計算することでZを取る確率が読み取れます。従って，あり得る混合戦略すべてがこの三角形に集まっていると言えます。

ということで，先の境目の三本の式を図示したのが，上の図の赤，青，緑の点線です。これら三つの直線が交わるのが中抜きの黒円で表した点\((x,y)=(1/4,1/4)\)です。ここで\(z=1-1/4-1/4=1/2\)であることと合わせると，オンライン・コンテンツ3.2の1節で求めた均衡\((x,y,z)=(0.25,0.25,0.5)\)と合致していることがわかります。これで境目が図示できましたが，もちろん境目をはさんだ，それぞれのサイドでどっちの選択肢の利得が高くなるかも必要です。先の方程式で片方のほうが他方よりも利得が高いという条件にして，利得の不等式を解くというのが一つの手段ではあります。しかしここでは利得表から直接見つけましょう。

たとえば青の直線，つまりYとZの境目について考えましょう。純粋戦略Yに対してはYは利得1を，Zは利得0を与えるので，YのほうがXよりも良いとわかります。図で言うと，純粋戦略Yを表す点\((0,1)\)ではYのほうがXよりも良いということです。ということは，この境目で分けて(0,1)を含むサイドではYのほうがXよりも良く，そしてその逆サイドではXのほうがYよりも良いのだとわかります。これを上の図に反映させて，境目のそばに同じ青でY,Xと書いておきました。Yと書いたほうがYのほうがXよりも良いサイドで，Xと書いたほうがXのほうがYよりも良いサイドということです。他の境目についても同様に各サイドでどちらの選択肢が他方よりも良いかを，境目の線と同じ色の字(X,Y,Zのようなセリフ体のフォント)で表しています。（ちなみに，これらの図では，どの戦略がその点・領域で良いかをセリフ体のフォントとし，\((1,0)\)が純粋戦略Xを表すように，その点が表している戦略をXや\((1,0)\)のようなローマン体のフォントとします。）

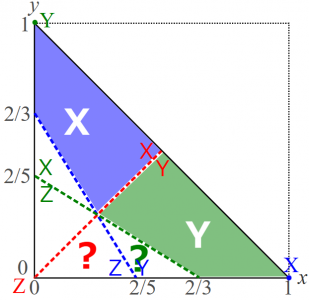
さて，ここから最適反応を見つけていきます。利得表で既に○をつけたように，純粋戦略X,つまり点\((1,0)\)では，最適反応はYです。なので，この3本の境目で分けた中の点\((1,0)\)を含む領域（下図の薄い緑の領域）では最適反応はYだとわかります。同様の発想で，純粋戦略Y，つまり点\(（0,1）\)を含む薄い青の領域では最適反応はXだとわかります。純粋戦略Z，つまり原点\(（0,0）\)は点線の上で今はまだ迷うかもしれませんね。そのように残っているところではどうなのでしょう？

そう，こうした領域をカバーするためにはきちんと，2戦略ごとの比較でエリアごとにどっちが良いかというのを見つけたのを積み重ねないといけません。たとえば上の図で白く残された中の緑の？マークがついた領域（青点線と緑点線と\(x\)軸に囲まれた領域）を注目しましょう。ここではXとYを比べる(赤)とYのほうが，またYとZを比べる（青）とやはりYのほうがよいので，Yが最適反応だとわかります。つまり薄い緑の領域と同じ最適反応だと言えます。薄い緑の領域との違いは，最適ではないXとZについてどちらがマシであるかということでしかありません。つまり，薄い緑の領域ではXのほうが，緑の？の領域ではZのほうが良いのですが，どちらもYよりも良くないので，Yが最適反応であることには影響しません。他方で，赤の？マークがついた領域では，青線の左なのでZがYよりも良くなっています。そして，また赤線の下なのでYはXよりも良いので，Z,Y,Xの順に良く，Zが最適反応で，Yはもはや最適反応ではないとわかります。

以上から，Yが最適反応なのは薄い緑の領域から緑の？の領域までだとわかったので，この二つの領域を緑の太線で下図では囲っています。同様にして，Xが最適反応となる領域を赤い太線で，Zが最適反応となる領域を緑の太線で囲っています。さらに，各領域で最適反応になっているものをやはり，その領域の色の文字（またセリフ体のフォント）で示しています。

この3つの最適反応の領域が触れ合うのが，赤・青・緑の点線の交点\((x,y)=(1/4,1/4)\)（中抜きの黒円）です。これはナッシュ均衡の一つでしたね。実際，この点はどの最適反応の領域にも入っているということは，X,Y,Zのどれも最適反応になっているということです。なのでこの点が意味する混合戦略\((x,y,z)=(0.25,0.25,0.5)\)は均衡になっています。また純粋戦略Zはナッシュ均衡でした。これを表す点\((x,y)=(0,0)\)はZが最適反応になる領域にあるので，これも均衡だと確かめられます。

オンライン・コンテンツ3.2の1節では，更にどのプレーヤーも\((x,y,z)=(0.5,0.5,0)\)としてXとYのみを使うのも均衡として求めました。これを表す点(x,y)=(1/2,1/2)（黒点）はXとYの最適反応の境目であり，使っているXとYは最適反応だとわかります。また\(x+y=1\)の線の上なので\(z=1-x-y=0\)なので最適になっていないZの割合はゼロです。なので，この点は均衡になっていると確かめられます。ちなみに，XとYの最適反応の領域の境目上の他の点では，戦略Zの割合がゼロになっていないので，Zも最適反応になる先ほどの\((x,y)=(1/4,1/4)\)を除いては均衡ではありません。

さらに\((x,y,z)=(0,2/3,1/3)\)はYとZの無差別条件と\(x=0\)から求めたのですが，均衡ではありませんでした。実際，これを表す点\((x,y)=(0,2/3)\)はYとZのどっちが良いかという境目（青点線）の上ではありますが，これは最適反応の境目ではないですね。実際，この点はXの最適反応の領域に中にすっぽり入っていて，使っている戦略Y，Zのどちらも最適反応ではありません。なのでこの点は均衡ではありません。

このように検討していくと，この図ではナッシュ均衡は以上で挙げた，純粋戦略Z，つまり\((x,y,z)=(0,0,0)\)，どれも使う\((x,y,z)=(0.25,0.25,0.5)\)，そしてXとYのみを使う\((x,y,z)=(0.5,0.5,0)\)だけだとわかります。ただし，この図を描くにあたって，プレーヤー1とプレーヤー2が同じ混合戦略を使うものにしぼっていることを思い出しましょう。なので，例えば利得表の○の組で示されているように，プレーヤー1が純粋戦略X，プレーヤー2が純粋戦略Yを使うのはナッシュ均衡であるにもかかわらず，この図には現れません。

2．最適反応動学

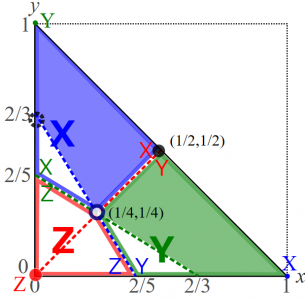
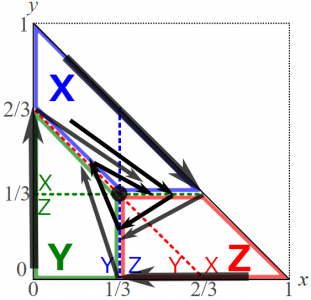
さて，これでこの図の中のどの点でも最適反応が何になるのかがわかりました。なので，最適反応動学でどこに向かうかがわかります。ただ前の図では最適反応となる戦略自体を各領域で書き込んでいましたが，より最適反応動学の行く先を直接ぱっと見てわかるようにしたいですね。なので，下の図では各領域での最適反応となる戦略を表す\((x,y)\)の点を書き込んでいます。

たとえば赤の太線で囲まれた領域では最適反応は純粋戦略Zでした。これは最適反応動学については，この領域からは純粋戦略Zを表す点\((0,0)\)に向かうことを意味します。上の図からわかるように，点\((0,0)\)からどのような方向にズレたとしても，赤の領域にとどまる限りは点\((0,0)\)に収束します。つまり，点\((0,0)\)は局所的に安定です。（ちなみに，「どのような方向」といっても，\(x,y,z\)が負になって戦略の割合として意味がなくなるような方向は考えません。）

他方で，緑の太線で囲まれた領域からは純粋戦略Yを表す点\((0,1)\)に，青の太線で囲まれた領域からは純粋戦略Xを表す点\((1,0)\)に向かいます。つまり，緑と青の領域については，一方から他方へと向かっていきます。もしも\(x+y=1\)の線ぴったりからなら，この線の上にある均衡の点\((1/2,1/2)\)へとまっすぐ収束していきます。より内側の点からは，まず青と緑の領域の境界になる\(x=y\)にたどり着きます。その後ですが，オンライン・コンテンツ4.1で詳しく説明したように，この境界をまたいで最適反応の向かう方向がぶつかるときには，境界上ではそのまま境界を滑るように動いていきます。つまり，このx=yの境界上を滑りながら点\((1/2,1/2)\)へと収束します。このように必ずしもまっすぐではないものの，やはり点\((1/2,1/2)\)からどのような方向にズレたとしても，結局は点\((1/2,1/2)\)へと収束するので，この点\((1/2,1/2)\)も局所的に安定です。

X,Y,Zのどれも取る\((x,y,z)=(0.25,0.25,0.5)\)という均衡を表す点\((x,y)=(1/4,1/4)\)からズレたとしましょう。赤の領域にズレると点\((0,0)\)へ，他の領域にズレたなら点\((1/2,1/2)\)へと，つまり他の均衡へと収束していき，点\((x,y)=(1/4,1/4)\)へは戻りません。従って，この点\((x,y)=(1/4,1/4)\)は均衡であるにもかかわらず不安定です。

言い換えると，このゲームにおいては最初の最適反応が純粋戦略Z（赤の領域）なら，そのままみんながZを取る均衡へ，最初の最適反応が純粋戦略XやY（青・緑の領域）なら，XとYが半々になる均衡へと収束していきます。そしてこれらの収束先の均衡は局所的安定である一方，X,Y,Zをどれも取る均衡\((x,y,z)=(0.25,0.25,0.5)\)は不安定だとわかりました。念のために申し添えておくと，このように最初の最適反応で収束先がきれいに決まるとは必ずしも限りません。特に，異なる初期状態から，最初の最適反応が同じであっても異なるところへと収束する（あるいはそもそも収束するかも異なる）ことはざらにあります。本文のモデル4.1がそうでした。

ところで，赤の領域と青・緑の領域の境界ちょうどに初期状態があったら，どこに行くのでしょう？上の図で例えば点\((2/5,0)\)からは緑の領域に入って\((0,1)\)に向かう矢印と，赤の領域に入って\((0,0)\)に向かう矢印の2本が描かれていますね。実際，\((2/5,0)\)から緑の領域，赤の領域それぞれにズレてると，その方向が唯一の最適反応なのでそっちへ向かっていきますね。つまり，境界をまたぐ2つの領域の最適反応がそれぞれ境界から遠ざかる方向に向かっています。これはオンライン・コンテンツ4.1の最後で説明した状況です。このときには境界ちょうどからはどちらの方向も，そして境界上を滑り続けることも，最適反応動学の「解」として許されます。つまり，初期状態がこの赤の領域と青・緑の領域の境界ちょうどになったらば，収束先は\((0,0)\)と\((1/2,1/2)\)のいずれも，そして不安定な\((1/4,1/4)\)にもなるわけです。

練習問題
オンライン・コンテンツ3.2の練習問題の（ア）で，2人のプレーヤーが対称的な（誰も骨折などしていなく同じ利得の構造の）ジャンケンのゲームを標準形で表し，均衡を示した。やはり，このジャンケンゲームをひとつの集団のポピュレーションゲームとしてとらえて，最適反応動学を図で分析し，均衡の安定性を判定せよ。

解答
グー，チョキ，パーそれぞれを出す確率を\(x,y,z\)とする。最適反応動学は以下のように描ける。唯一のナッシュ均衡は\((x,y,z)=(1/3,1/3,1/3)\)であり，それを表す点\((1/3,1/3)\)は大域的に安定である。