最適反応動学の数式

PDFファイル

【図斎　大】

1. 最適反応動学の微分方程式（とりあえず）

最適反応動学を数式で表すにあたって，まず「動き」というものが数式でどう表されるかをおさえておきましょう。そのために\(x\)を考察の対象となるものの状態（最適反応動学ならプレーヤーたちの戦略の組）としましょう。それが時間とともに変わるので，時間を表す変数を\(t\)とすると，\(x\)は\(t\)の関数だと言えます。そして，時間\(t\)が連続的に変わっていくときに，状態\(x\)も徐々に変わっていくとしたときに，その変化を

\[ \dot{ x } =f(x) \tag{ODE} \]

というような微分方程式でよく表します。ここで\(\dot{ x }\)は状態\(x\)の時間\(t\)に関する微分\(dx/dt\)を表し，瞬間的な動きを表します。従って，\(\dot{ x } =f(x)\)はこの瞬間的な動きが，現在の状態\(x\)の関数\(f(x)\)で決まるということを意味しています。

最適反応動学では，現時点の戦略の組から最適反応の戦略の組へとまっすぐむかっていきます。なので，現時点の戦略の組を\(x\)，最適反応の戦略の組を\(b(x)\)と置いて，

\[ \dot{ x } =λ\{b(x)-x\} \tag{BRD} \]

と（とりあえず）表せます。（実は数学的に細かい話を考えると例外が出るので，ここから先「とりあえず」ということで例外を省いた肝を説明していきます。）ここで\(λ\)は戦略改訂の速さを表す，正の数のパラメータです。

本文のモデル4.1で最適反応動学を図示した図4-3を振り返りましょう。（ここから先は教科書の本文を開けながら読んでみてください。）たとえば点\((0.2,0.8)\)から延びている黒矢印が，現状の戦略の組\(x=(0.2,0.8)\)から最適反応動学で進む\(\dot{ x }\)です。これはこの点\((0.2,0.8)\)から最適反応である\((1,0)\)へ伸びた灰色の直線上にあります。\(b(x)\)はこの\((1,0)\)という最適反応（正確にはそれのみを含む集合）を指すので，この直線がまさに\(b(x)-x\)が表すものです。それを\(λ\)で縮めたものがまさに黒矢印で示される\(\dot{ x } \) なので，上の式と合っていますね。他の点でも同様に確かめてみましょう。

このように式(BRD)で定められた\(\dot{ x }\)という毎瞬間の動きをつなげたものが最適反応動学の経路だと（とりあえず）言えます。つまり，数学的には(BRD)の式で与えた時間微分\(\dot{ x }\)を初期値から現時点まで積分したもので，その時点での\(x\)がわかります。これが，図4-4で矢印をどんどん伸ばして，経路を描いたことに相当します。そして，微積分の基本定理によると，これは逆に言うと，この積分して作った\(x\)はまさに微分方程式(BRD)の「解」に（とりあえず）なっています。

2. 最適反応動学の「解」

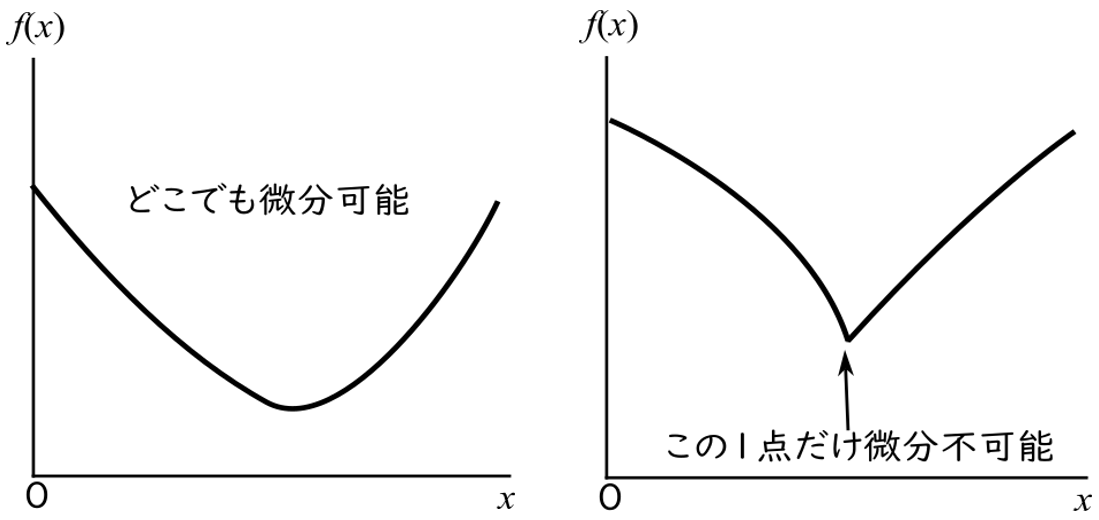
微分方程式を数学のほうできちんと勉強した，あるいは微分の意味をよく理解している人は，この図4-4を見ると，奇妙なことに気づくかもしれません。「微分」というのは左の図のような滑らかなグラフで接線を一本引くことに相当し，右の図のＶの字の谷底の点のようにカキっと折れたところでは，そもそも微分できません。

図4-4では最適反応が切り替わるところで，カキっと折れてしまっていますね。つまり，その折れる瞬間は微分できていないはずです。なのにこの経路を微分方程式(BRD)の「解」というのはどういうことでしょう。

かなりマニアックな（最適反応動学に関する研究をしてないと，ゲーム理論の専門家でもなかなか触れない特殊な）数学なのですが，この「解」について，最適反応動学では普通の微分方程式の解よりもちょっとだけ緩くとらえます。どういうことかというと，普通の微分方程式(ODE)では\(x\)が「解」というときには，\(x\)が常に微分可能で，その上で\(x\) が常に方程式（ODE）を満たすことを意味しています。しかし，ここでは微分可能でないことも例外的に一瞬だけ（というのがつながらないなら何回も，つまり加算無限回だけ）認め，その微分可能なときに(BRD)式を満たすことを「解」といいます。（このような「解」をカラテオドリの解と言います。空手踊りではなくConstantin Carathéodoryという数学者の名前から来ています。）

なぜこんなことをしないといけないかというと，(BRD)式での最適反応\(b(x)\)のせいです。境目のところでたとえば\(p=1\)から\(p=0\)のようにジャンプして（不連続に）変わりますね。これは最適反応の戦略が二つの純粋戦略の間で切り替わることに相当します。そして「極端な性質」を思い出すと，この境目では，その二つの純粋戦略だけではなく，その二つを混ぜたどんな混合戦略も最適反応になるのでした。ということは，ジャンプする瞬間には\(p=1\)と\(p=0\)だけでなく，その間のどんな\(p\)も，\(p=0.1\)も\(p=0.8077878\)もどれも最適反応になるということなのです。つまり\(b(x)\)がひとつに定まらないので，(ODE) 式のように「\(x\) の値を与えると右辺でもって \(\dot{ x } \)がひとつ定まる」というようにいかないことが最適反応だとありえます。すなわち，最適反応動学では，まず連続でない，そしてそもそも一つに方向が定まらない，ということで，普通の微分方程式のようにすぱっとした（常に式を満たすような）解までは要求できないのです。（もしかすると\(b(x)\)はひとつに定まらないのなら，\(b\)は（ODE）式の\(f\)のような関数ではないだろうと気づいたかもしれません。そう，最適反応は複数ありえる，つまり集合を成すので，最適反応動学を正確に定義するときには，集合の値を取る微分方程式，すなわち微分包含(differential inclusion)というものを考えます。これに関してはブックガイドで挙げたSandholm(2010)を参考にしてください。）

3. 最適反応の境目 （マニアックな話）

ともかく，このように「解」となる条件を緩めることで，図4-4のような折れ線の経路も(BRD)の解と言うことになるのです。ここまではあくまで本文で説明したような最適反応動学の経路を図から直接描くやりかたを数式で別に言い換え，数学的に正当化しただけです。ここではさらに，本文では出てこなかった問題もついでにここでおさえておきましょう。以下の点を深く掘り下げるのは，進化動学や最適反応動学のエッセンスというよりも，まれに遭遇するかもしれない細かい点を完全にするための議論になっていきます。（ただ数理的には面白いところです。）ゲーム理論家の中でもこの分野を研究するものでないと馴染みのない話になっていきますし，そういうところで丁寧な説明がないと納得しづらいということもあろうかと詳しく述べておきます。しかし，本文を読み本文中の問題を解く，そして進化動学のコアなアイデアを理解するにはそこまで踏み込まなくとも十分です。他のオンライン・コンテンツや追加問題で例外的に以下のような状況も出てきますが，端的には以下の二つの２小節3.1と3.2の最後の段落のまとめ（特に下線を引いた箇所）を「境目ちょうどで例外的に判断しづらい時にきちんと解きたいならどうすればいいのか」の方針として知っておけば十分です。

3.1 境目で進む方向がぶつかり合うとき

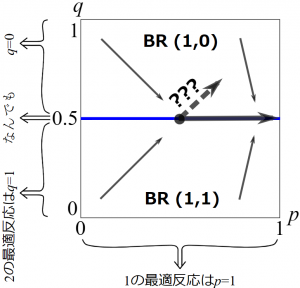
下の図では\(\rm{BR(1,0)}\)と記された上の領域では右下へと，\(\rm{BR(1,1)} \)と記された下の領域では右上へと進もうとしています。（\(p\)はプレーヤー１の混合戦略，\(q\)はプレーヤー２の混合戦略としよう。）

以下の数理的分析には不要ですが，この図の背後にあるゲームとしては以下のようなポピュレーションゲームを考えます。人々はプレーヤー１側と２側のいずれかに属し，最適反応動学に従いAとBのいずれかの選択を徐々に変えていきます。\(p,q\)はそれぞれの側でのAを取る人の割合。プレーヤー１側では（\(p,q\)によらず）Aは利得1を，Bは利得0を与えるとします。なので，Aが強く支配する戦略であり，最適反応は\(p=1\)となります。プレーヤー２側では，Aを取ると（同じプレーヤー側の中のBを選択する者と会ったときに利得１を獲得するものとして）期待利得が\(1-q\)，Bを取ると（同じプレーヤー側の中のAを選択する者と会ったときに利得１を獲得するものとして）期待利得が\(q\)とします。そうすると\(q\lt0.5\)で最適反応はAの純粋戦略(\(q=1\)), \(q>0.5\)で最適反応はBの純粋戦略(\(q=0\))，\(q=0.5\)でAとBのどんな混合戦略も最適反応となります。

青線で描かれた二つの境目となる\(q=0.5\)では，\(q=0.5\)を維持したまま\(p=1\)のほう，つまり右の方へと青線の上を滑って動いていますね。これはどういうことでしょう？プレーヤー１に関しては，上で述べたようにたしかに\(p=1\)は最適反応です。プレーヤー２に関しては「\(q=0.5\)でAとBのどんな混合戦略も最適反応」なのでした。なので，たしかに\(q=0.5\)も最適反応のひとつではあります。なので， \((1,0.5)\)もここで取っている最適反応の組\(b(x)\)とすると，この青線を滑る経路は（BRD）式を満たしていることになります。

他方で，他の最適反応の組を青線でとってみるとどうでしょう？たとえば灰色の矢印は\((1,1)\)に向かっていますね。これはプレーヤー１の最適反応として\(p=1\)に，プレーヤー２の最適反応として\(q=1\)を取っていることになります。プレーヤー２はどんな\(q\)も青線では最適反応なのでこれも許容されるはずですね。しかしこの方向に進んだ次の瞬間には青線の上の領域に入ります。するとプレーヤー２の最適反応は\(q=0\)のみであり，\(b(x)\)は\((1,0)\)しか取れません。従って右下に進むしかなく，青線へとまた押し戻されます。すなわち，青線から(1,1)へと向かう経路は，青線にいる一瞬では（BRD）を満たすものの，ひとたび離れた瞬間に，周りの領域の最適反応と合わないので（BRD）式を満たさなくなり，最適反応動学の解にはなりません。

すなわち，このように最適反応の境目をまたぐ二つの領域で最適反応動学の進む方向がぶつかり合うときには，その境目にとどまることになります。それでも一点にとどまるのでなく，滑るように動くのは，この境目で最適反応が切り替わるのとは別のプレーヤーの最適反応のおかげです。上の図の青線でも，プレーヤー１は（この青線の上を含みどちらの領域でも）\(p=1\)が最適反応になっています。従って，\(\boldsymbol{p} \)に関しては，\(\boldsymbol{p=1}\)に向かって着実に進んでいきます。従って，二人の戦略の組\((p,q)\)は，\(p=1\)のほう，つまり右の方へと青線の上を滑って動いていくのです。

3.2 境目で進む方向がしりぞけ合うとき

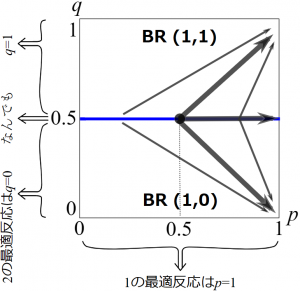
下の図では先の例とは逆に，\(\rm{BR(1,1)}\)と記された上の領域では最適反応の組が\((1,1)\)であり右上へと，\(\rm{BR(1,0)}\)と記された下の領域では最適反応の組が\((1,0)\)であり右下へと進もうとしています。つまり青色の境界線をまたぐ二つの領域で最適反応動学の進む方向がしりぞけ合っています。

特に点\((0.5,0.5)\)からは，右上へ進む矢印，青線上を滑る矢印，右下へ進む矢印の3本が描かれています。実は（BRD）の解としては，このどれもが許されます。つまり，この点\((0.5,0.5)\)は，まっすぐ\((1,1)\)へ収束することも，また青線上を滑って\((1,0.5)\)へ収束することも，そして\((1,0)\)へ収束することのどれもありえるのです。先の例では青線を滑るしかありませんでした。違いは何でしょう。

先の例でも右上に進む\((1,1)\)も，青線上を滑る\((1,0.5)\)も，右下へ進む\((1,0)\)もどれも，この青線上では最適反応の組としてありえました。それはここでも同じです。ただ先の例では青線からひとたび離れたときに，青線へと戻る方向のみが最適反応なので，またすぐに青線へと戻されるのでした。

しかしここでは境界の外の最適反応は境界から離れる方向になっています。たとえば点\((0.5,0.5)\)から最適反応として\((1,1)\)をとって右上へ進んだとしましょう。青線を離れるや否や，上の領域に入りますが，そこでも最適反応の組は \((1,1)\)です。従ってこのまま\((1,1)\)を最適反応として取り続け，右上へと進みます。なので， \((1,1)\)をこの経路で取る最適反応の組\(b(x)\)とすると，点\((0.5,0.5)\)から右上の\((1,1)\)へと進む経路は（BRD）式を満たしていることになります。同様にして，点\((0.5,0.5)\)から下の領域に入り右下の\((1,0)\)へと進む経路も，\((1,0)\)を下の領域でも最適反応の組\(b(x)\)として取り続けられるので（BRD）式を満たします。そして，この境界ピッタリにおいては\(q=0.5\)も(\(q=0\)や\(q=1\)，そしてどんな\(q\)も)プレーヤー2の最適反応になるというのは先の例と同じです。従って，やはり青線の境界を滑って\((1,0.5)\)へ進む経路も，\((1,0.5)\)を最適反応の組\(b(x)\)として取り続けられるので（BRD）式を満たします。ということで，このどの経路も最適反応動学の「解」なのです。

この理屈は，点\((0.5,0.5)\)に限らず，上図の境界上の点のどこでも言えますね。ということは，点\((0.5,0.5)\)からしばらく境界上を進んで点\((0.8,0.5)\)あたりに来たとしたときに，その点\((0.8,0.5)\)でも言えるわけです。つまり，ここに来てからも，境界上を滑り続けるだけでなくて，また改めて右上の\((1,1)\)や右下の\((1,0)\)に向かって動き始めることも，（BRD）の解として許されるのです。ということは，もともとの出発点\((0.5,0.5)\)から始めたときの経路は，

• すぐに右上の\((1,1)\)へとまっすぐ進んでいく
• すぐに右下の\((1,0)\)へとまっすぐ進んでいく
• 青線上を真右にずっと進んで\((1,0.5)\)へとまっすぐ進んでいく

だけでなく，

• 青線上を真右に「しばらく」進んでから，右上の\((1,1)\)へと向きを変え，後はまっすぐ進んでいく
• 青線上を真右に「しばらく」進んでから，右下の\((1,0)\)へと向きを変え，後はまっすぐ進んでいく

というのも，すべて最適反応動学の「解」になります。さらに，この「しばらく」というのは，上述の点\((0.8,0.5)\)に着くまでとは限らず，もっと早く点\((0.50001, 0.5)\)に着いたらとか，もっと後の点\((0.99999, 0.5)\)に着いてからでもよいのです。なので，点\((0.5,0.5)\)と初期状態をひとつに定めても，「解」は無数に存在します。

まとめると，最適反応の境目をまたぐ二つの領域で，最適反応動学の進む方向がしりぞけ合う状況では，その境目で滑るだけでなく，境目からそれぞれの領域の中へと入っていくという，どの経路も最適反応動学の解になります。しかも，境目の上を滑って行ってもこの状況が変わらないのなら，しばらく滑った後のどこでも，改めてそれぞれの領域の中へと入り始めるという経路も，解になります。普通の微分方程式なら「解」となる経路は必ず一つに定まるのですが，最適反応動学では最適反応の境目で不連続になるために，このように複数の「解」の経路も出てくることがあります。

注記）さらに，似たような状況で，収束する軌道と収束しない軌道とが一つの初期状態から生まれるということもあります。興味のある方はSandholm (2010)のExample 5.1.7を参照してください。また，最適応答にわざわざ変えるインセンティブを考慮することで，あまりにも変な経路を減らそうというのが，手前味噌ですがZusai (2019) で考えた「緩和された最適反応動学」(tempered best response dynamics)のアイデアです。深入りすると，進化動学の中でも最適反応動学を専門とする研究者のさらにマニアックな議論にはまり込んでしまうので，ここではやめておきましょう。取り合えずそういうこともあるという程度に頭の中に入れておいて，このような状況に遭遇したときに迷わずにこの文書を見直せば大丈夫かと感じていただければ十分です。

参考文献

• Sandholm, W.H. (2010) Population Games and Evolutionary Dynamics, MIT Press.
• Zusai, D. (2018) “Tempered best response dynamics.” International Journal of Game Theory, 47 (1), pp.1-34.