【小俵将之・浅古泰史・森谷文利・図斎大】
問題8.1(モデルの設定の変更)
(注)純粋戦略のみを考える。プレーヤーが行動を確率的に取っているような完全ベイジアン均衡は求めない。
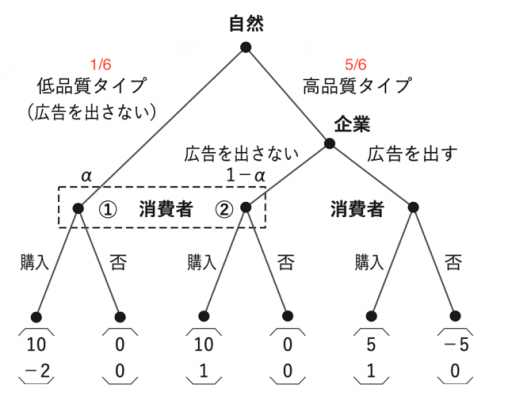
(ア)ゲームの木は以下のようになる。
まず後ろ向き帰納法で解ける部分を解くと,消費者は右の「広告を出す」の後の情報集合(1つの意思決定点しか含んでいない)では「購入」を選ぶことが分かる。
消費者の左側の情報集合に到達する前のプレーヤーである,高品質タイプの企業が取りうる行動は「広告を出す」,「広告を出さない」の2通りある。
「広告を出す」と整合的な消費者の信念は\(α=1\)である。この信念の下での,左の情報集合における最適反応は「購入しない」である。高品質タイプ企業の「広告を出す」は,消費者の
\[(左の情報集合での行動,右の情報集合での行動)=(購入しない,購入する)\]
という戦略に対する最適反応になっている。よって,
\[((広告を出す,(購入しない,購入する);α=1)\]
は完全ベイジアン均衡である。この均衡では,低品質企業と高品質企業は異なる行動を取っている。よって,事前確率に関わらず消費者の信念は\(α=1\)になり企業のタイプを見極めることが出来る。
次に,企業が広告を出さない均衡を探す。高品質タイプ企業の「広告を出さない」という行動と整合的な信念は\(α=1/6\)である。この信念の下での,左側の情報集合における最適反応は「購入する」である。
高品質タイプ企業の「広告を出さない」は,消費者の(購入する,購入する)に対する最適反応になっている。よって
\[ \left( (広告を出さない,(購入する,購入する);α=\frac{1}{6} \right) \]
は完全ベイジアン均衡になる。まとめると,完全ベイジアン均衡は以下の2つである。
\[ \bf{ ①\left( (広告を出す,(購入しない,購入する);α=1 \right) } \]
\[ \bf{ ②\left( (広告を出さない,(購入する,購入する);α=\frac{1}{6} \right) } \]
このうち,②の均衡は高品質タイプである確率が50%のときには存在していなかった。本問題の設定下では,消費者は企業が高品質タイプである可能性が高いと思っている。よって,たとえ両タイプともに広告を出さなかったとしても,消費者は「高品質タイプである可能性が高い」と信じて購入してくれるため,わざわざ広告を出す必要が無い。よって,広告を出さない均衡が存在する。
ただし,このような状況下でも①の広告を出す均衡が存在することには注意してほしい。高品質タイプが広告を出す場合,消費者は「広告を出さない企業は低品質タイプのはずだ」と信じていることになる。このような状況下で低品質タイプと勘違いされないためには,高品質タイプは広告を出すしかない。
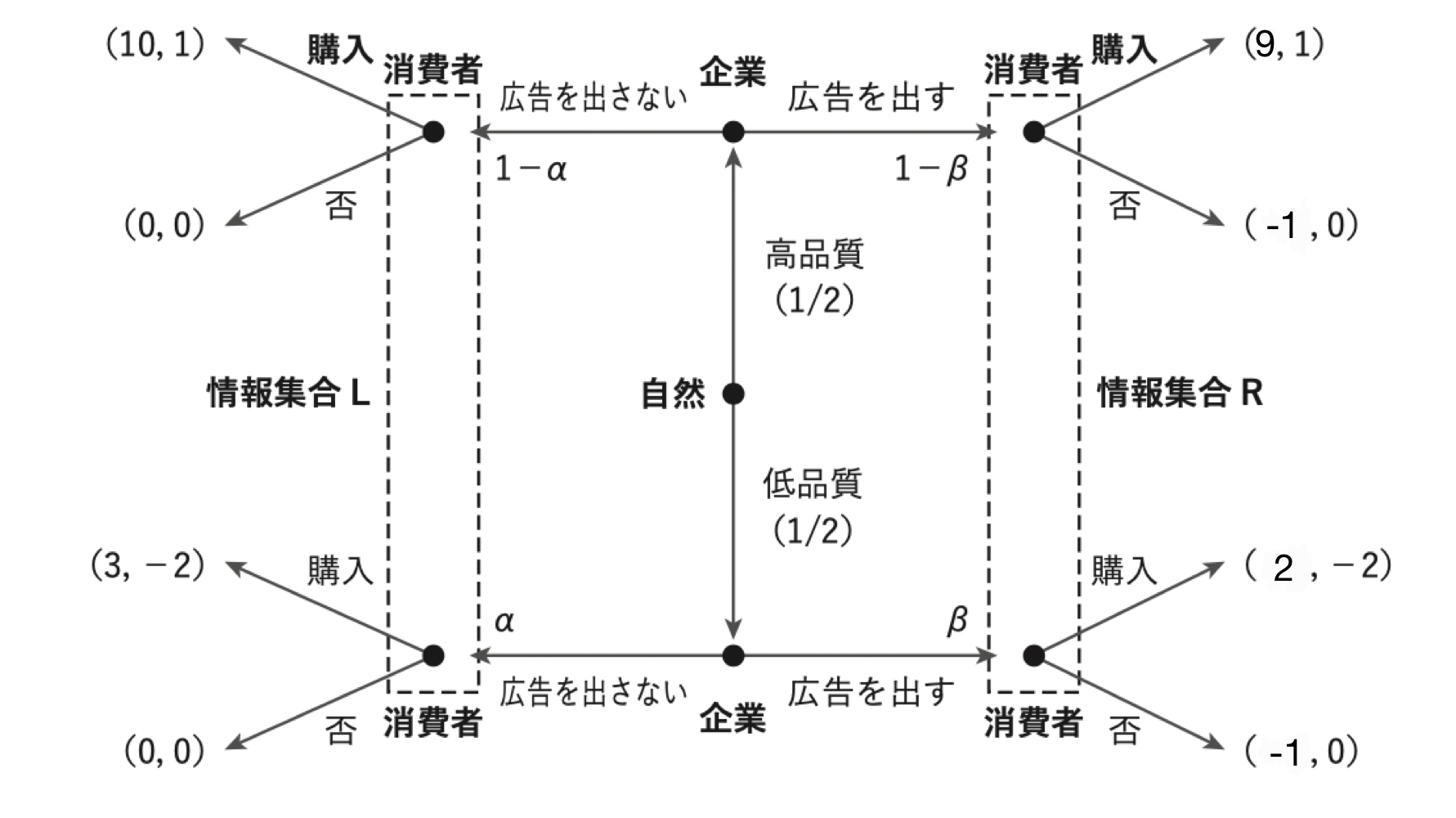
(イ)ゲームの木は以下のようになる。
企業には高品質タイプと低品質タイプがいるので,企業の戦略=(高品質タイプ企業の行動,低品質タイプ企業の行動)は以下の4通りある。
ⅰ.(広告を出す,広告を出さない)
ⅱ.(広告を出さない,広告を出す)
ⅲ.(広告を出す,広告を出す)
ⅳ.(広告を出さない,広告を出さない)
次に,それぞれの戦略が完全ベイジアン均衡(の一部)になるかを調べる。
ⅰ.(広告を出す,広告を出さない)
(広告を出す,広告を出さない)と整合的な消費者の信念は\(α=1,β=0\)である。つまり消費者は企業の行動を観察することでタイプを完全に見分けられている。見分けられているため,消費者の最適反応は「情報集合Rでは購入して情報集合Lでは購入しない」となる。つまり,消費者は「広告を出している企業は高品質に決まっているので購入するが,広告を出してない企業は低品質に決まっているので購入しない」と思っていることになる。すると,今度は企業の(広告を出す,広告を出さない)という戦略がこの消費者の戦略に対する最適反応にならなくなる。何故なら低品質タイプの企業は「広告を出す」に逸脱することで,期待利得を0から2まで上げられるからである。よって(広告を出す,広告を出さない)は均衡にならない。
ⅱ.(広告を出さない,広告を出す)
ここでも,i. の場合と全く同じ理由で(広告を出さない,広告を出す)は均衡にならない。今回の場合も企業の戦略から消費者は企業のタイプを完全に見分けられている。ただし今回は消費者は「広告を出さない企業は高品質に決まっているので購入するが,広告を出している企業は低品質に決まっているので購入しない」と思っている。このとき低品質タイプの企業は「広告を出さない」に逸脱することで得をする。よって,(広告を出さない,広告を出す)は均衡にならない。
ⅲ.(広告を出す,広告を出す)
どちらの企業も広告を出していた場合,情報集合Lには到達せず,情報集合Rには確実に到達する。この戦略と整合的な情報集合Rの信念は\(β=1/2\)である。消費者にとって「購入する」からの期待利得は
\[\frac{1}{2} \cdot (-2)+\frac{1}{2} \cdot 1=-\frac{1}{2}\]
であるが,「購入しない」からのそれは0であるため,\(β=1/2\)の下での消費者の最適反応は「購入しない」である。しかし,(広告を出す,広告を出す)は情報集合Rにおける「購入しない」に対する最適反応になっていない。何故なら,情報集合Rで「購入しない」が選ばれているとき,高品質タイプ企業は広告を出せば期待利得は\(-1\)になるが,「広告を出さない」を選べば最低でも\(0\)の期待利得を得るからである。よって両タイプの企業が広告を出す戦略の組は均衡にならない。
ⅳ.(広告を出さない,広告を出さない)
どちらのタイプの企業も広告を出していないとき,情報集合Rには到達せず情報集合Lに確実に到達する。情報集合Lにおける整合的な信念は\(α=1/2\)であり,\(α=1/2\)の下での情報集合Lでの最適反応は「購入しない」である。(広告を出す,広告を出す)が均衡で取られている為には,消費者は経路外の情報集合Rで「購入しない」を選んでいなくてはならない。何故なら,もし情報集合Rで「購入する」を選んでいるならば(例えば)高品質タイプの企業は「広告を出す」に逸脱することで期待利得を0から9に上げられるからである。よって,情報集合Rでの最適反応が「購入しない」になるように経路外の信念\(β\)を定めてやれば
\[ \left( (広告を出さない,広告を出さない),(否,否), α= \frac{1}{2}, β \right) \]
は完全ベイジアン均衡になる。情報集合Rで「購入する」を選べば消費者は
\[-2β+1-β\]
の期待利得を得る。一方,「購入しない」を選べば0になる。よって「購入しない」が最適反応になる\(β\)の条件は以下で与えられる。
\[2β+1-β≤0⇔1/3≤β.\]
よって,
\[ \bf{ \left( (広告を出さない,広告を出さない),(否,否) ;α=\frac{1}{2}, β \right) ただし \frac{1}{3}≤β } \]
は完全ベイジアン均衡である。
本問題では広告の費用が非常に低くなっており,高品質タイプだけではなく,低品質タイプも,(消費者が買ってくれるのであるならば)広告を出しても正の利得を得ることができている。よって,広告を出すことで消費者が購入してくれると見こせるならば,高品質タイプだけではなく,低品質タイプも広告を出すインセンティブを持つことになる。このような状況下では,広告を通して企業のタイプを見分けることはできない。その結果,広告はシグナルとしての機能を果たさなくなる。シグナルとして機能するためには,一方のタイプが十分に高いシグナル費用を有している必要があることがわかる。
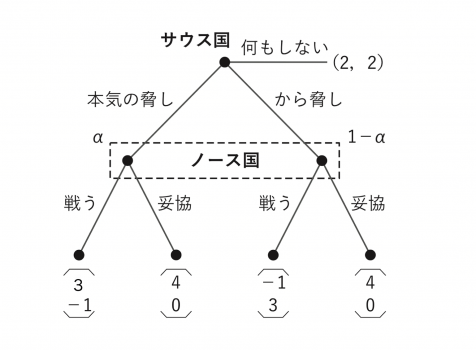
(ウ)ゲームの木は以下のようになる。
サウス国が「何もしない」を選ぶのは均衡にならない。何故なら経路外でノース国が「戦う」と「妥協」のどちらを選んでいようとも,「本気の脅し」を選ぶことでサウス国は最低でも3の期待利得を得ることができるからである。
サウス国が「から脅し」を選んでいるのは均衡にならない。まず「から脅し」に対する整合的な信念は\(α=0\)であり,この信念の下でのノース国の最適反応は「戦う」である。しかし,ノース国が「妥協」を選んでいるならばサウス国は「本気の脅し」に逸脱することで,期待利得を\(-1\)から\(3\)まで上げられる。よって,サウス国が「から脅し」を選んでいるのは均衡にならない。
サウス国が「本気の脅し」を選んでいるのは均衡になる。まず「本気の脅し」に対する整合的な信念は\(α=1\)であり,この信念の下でのノース国の最適反応は「妥協」である。そしてサウス国の「本気の脅し」は「妥協」に対する最適反応になっている。よって
\[((本気の脅し,妥協); α=1)\]
は完全ベイジアン均衡である。
モデル8.3では,ノース国が「戦う」を選んでいる限り,「何もしない」がサウス国の最適な戦略であったため,「何もしない」を選ぶ均衡が存在した。しかし,本問題では準備の費用がかからないことから,ノース国が「戦う」を選んでも「本気の脅し」を選ぶことが最適になっている。よって,均衡では本気の脅ししか選ばれない。脅しの信憑性を高めるという意味では,争いへの準備費用が十分に低いと思われていることも大切なようである。
問題8.2(誰が情報を持っているか)
(注) 純粋戦略のみを考える。プレーヤーが行動を確率的に取っているような完全ベイジアン均衡は求めない。
(ア)プレーヤー2の情報集合の内,左の意思決定点にいる確率を\(α\)と書くとする。プレーヤー2の情報集合に到達する前に,プレーヤー1が左の情報集合でAかBを選び,右の情報集合でCかDを選んでいる。よって,プレーヤー2の情報集合に到達する前のプレーヤーの戦略は以下の4通りある。
- (A,C)
- (A,D)
- (B,C)
- (B,D)
-
それぞれの戦略に対するプレーヤー2の整合的な信念\(α\)は以下の通りである。
- (A,C)
- \(α=1/2\)
- (A,D)
- \(α=1\)
- (B,C)
- \(α=0\)
- (B,D)
- プレーヤー2の情報集合には到達しない。
それぞれの信念の下でのプレーヤー2の最適反応は以下の通りである。
- (A,C)
- \(α=1/2\)の下でのプレーヤー2の最適反応はX。
- (A,D)
- \(α=1\)の下でのプレーヤー2の最適反応はX。
- (B,C)
- \(α=0\)の下でのプレーヤー2の最適反応はY。
- (B,D)
- \(α>2/5\)ならば最適反応はX,\(α<2/5\)ならば最適反応はY。\(α=2/5\)ならばXもYも最適反応。
はじめに提示したプレーヤー1の戦略(A,C),(A,D),(B,C)が,上で求めたプレーヤー2の最適反応に対する最適反応になっているかを確認する。(B,D)については個別に議論する。
- (A,C)
- プレーヤー2の最適反応はXであるが、Xに対してAは最適反応でない。
- (A,D)
- プレーヤー2の最適反応はXであるが、Xに対してAは最適反応でない。
- (B,C)
- プレーヤー2の最適反応はYであるが、Yに対してBは最適反応でない。
よってプレーヤー1が(A,C),(A,D),(B,C)のいずれかをとっているような完全ベイジアン均衡は存在しない。
次にプレーヤー1が(B,D)をとっているような完全ベイジアン均衡を探す。このような均衡においては,プレーヤー2はXを取っていなくてはならない。何故なら,もしプレーヤー2がYを取っているならば(B,D)はYに対する最適反応にならないからである。情報集合の左側の意思決定点に到達しているという信念を\(α\)とすれば,\(α≥2/5\)のときXがプレーヤー2の最適反応になる。このとき\( \rm ((B,D),X,α)\)は完全ベイジアン均衡になる。よって,以下の戦略の組と信念は完全ベイジアン均衡である。
\[ \bf{ ((B,D),X,α) ただしα≥2/5 .} \]
(イ)まず後ろ向き帰納法で解ける箇所を先に解く。すると均衡ではプレーヤー2は左の情報集合ではX,右の情報集合ではYを選んでいる。
プレーヤー1の情報集合に到達する前に行動するプレーヤーはいない。従ってプレーヤー1の信念は他のプレーヤーの戦略には依存せず,自然が定める確率のみによって決まる。
次に,プレーヤー2の最適反応を所与としてプレーヤー1の最適反応を求める。Aを選べば
\[ \frac{1}{2} \cdot 0+\frac{1}{2} \cdot 6=3\]
の期待利得を得る。一方,Bを選べば2である。よって,プレーヤー1の最適反応はAである。
以上より,完全ベイジアン均衡は
\[ \bf{(A,(X,Y))} \]
である。
問題8.3(ゼルテンの馬)
(注)純粋戦略の完全ベイジアン均衡のみを考える。プレーヤーが行動を確率的に取っているような均衡は扱わない。
- プレーヤー1がD,プレーヤー2がaを選んでいるような均衡は存在しない。もしプレーヤー3が(D,a)と予想していた場合,この予想と整合的なプレーヤー3の信念は,「確率1で左の意思決定点にいる」である。この信念の下でのプレーヤー3の最適反応はLである。しかし,プレーヤー2のaはLに対する最適反応になっていない。よってプレーヤー1がD,プレーヤー2がaを選んでいるような均衡は存在しない。
- プレーヤー1がA,プレーヤー2がdを選んでいるような均衡は存在しない。もしプレーヤー3が(A,d)と予想していた場合,この予想と整合的なプレーヤー3の信念は,「確率1で右の意思決定点にいる」である。この信念の下でのプレーヤー3の最適反応はRである。しかし,プレーヤー2のdはRに対する最適反応になっていない。よってプレーヤー1がA,プレーヤー2がdを選んでいるような均衡は存在しない。
- プレーヤー1がD,プレーヤー2がdを選んでいるような均衡は存在しない。もしプレーヤー3が(D,d)と予想していた場合,この予想と整合的なプレーヤー3の信念は,「確率1で左の意思決定点にいる」である。この信念の下でのプレーヤー3の最適反応はLである。しかし,プレーヤー1のDは(d,L)に対する最適反応になっていない。よってプレーヤー1がD,プレーヤー2がdを選んでいるような均衡は存在しない。
- プレーヤー1がA,プレーヤー2がaを選んでいるような均衡は存在する。もしプレーヤー3が(A,a)と予想していた場合,プレーヤー3の情報集合には到達しないので,どんな信念もこの予想と整合的になる。均衡で(A,a)が取られるためには,プレーヤー3はRを取っていなければならない。何故ならaはLに対する最適反応ではないからである。プレーヤー3のRが最適反応になるように,均衡経路外の信念を設定してやれば(A,a,R)は完全ベイジアン均衡になる。信念を右側の意思決定点にいる確率αで表す。Rが最適反応なるためには\(α≥2/3\)でなくてはならない。よって,以下が均衡となる。
\[ \bf{(A,a,R;α) ただし } \boldsymbol{ α≥2/3 } \]
- (A,C)