【小俵将之・浅古泰史・森谷文利・図斎大】
問題1.1(モデルの設定を変える)
(ア) 容疑者Xの献身
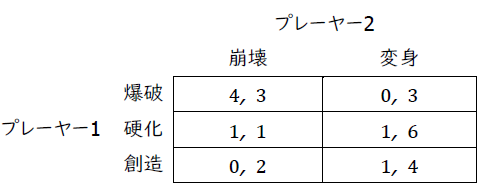
容疑者XはYの刑期の最小化を目的としている。よって,容疑者Yだけではなく,容疑者Xも容疑者Yの刑期に-1をかけたものを利得としている。よって,図1-1の利得表は以下のように書き換えられる。
容疑者Xにとって,容疑者Yが黙秘した場合には黙秘の方が(-3>-10),容疑者Yが自白を選んだとしても黙秘の方が(0>-6),利得が高い。よって,容疑者Xの支配戦略は,「黙秘」である。他方,容疑者Yの支配戦略は「自白」のままである。以上から,両プレーヤーが支配戦略を選択すると考えられるため,予測される結果は容疑者Yのみ自白する(黙秘,自白)になる。また,他のいかなる戦略の組に変更しても,利得が0からマイナスの値に低下しているので,(黙秘,自白)はパレート最適である。ちなみに本問題は,東野圭吾氏の小説『容疑者Xの献身』をモチーフにしている。原作では,どのような均衡が生じているのか,興味がある読者は読んでみてほしい。
(イ) 嫉妬する企業
ここでは,「自分の利潤-相手の利潤」が利得になる。よって,(高価格,高価格)や(低価格,低価格)の場合には利潤差はないため,両企業ともに利得はゼロになる。一方で,片方のみ高価格を設定した場合,低価格を設定した企業との利潤差は12であるため,高価格を設定した企業の利得は-12であり,低価格を設定した企業の利得は12になる。以上より,図1-9の利得表は以下のように書き換えられる。
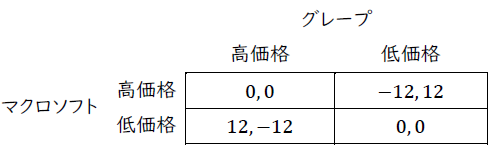
マクロソフトにとって,グレープが高価格を選んだ場合には低価格の方が(12>0),グレープが低価格を選んだとしても低価格の方が(0>-12),利得が高い。よって,マクロソフトの支配戦略は,「低価格」である。グレープも同様の理由から,支配戦は「低価格」である。以上から,両プレーヤーが支配戦略を選択すると考えられるため,予測される結果は(低価格,低価格)になる。
また,(低価格,低価格)から(高価格,高価格)に戦略の組が変わっても,両プレーヤーの利得は変わらない。(低価格,低価格)から(高価格,低価格)に変わった場合には,マクロソフトの利得は,0から-12に低下する。(低価格,低価格)から(低価格,高価格)に変わった場合には,グレープの利得が0から-12に低下する。よって,いかなる戦略の組に変更しても,利得が変わらない,あるいは低下するため,(低価格,低価格)はパレート最適である。
企業の嫉妬を考えても,表1-9の結果と変わらない。また,他社と同一の利潤であれば満足であるため,表1-9と異なり,利潤は低いにもかかわらずパレート最適な結果になっている。嫉妬するという一見現実的と思われる設定を入れても,結果が変わらない上に,パレート最適性に関しては少し奇妙な結論になっている。寡占市場の分析において「嫉妬」の存在は,それほど重要ではないと言えるのではないだろうか。
(ウ) 成功した時の利得が大きいときのチーム評価
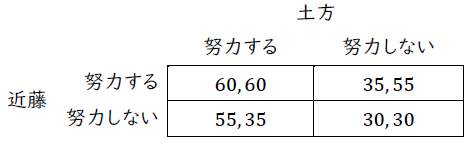
両者とも努力してプロジェクトが大成功した場合には80を受け取るため,利得は80-20=60になる。(大成功ではないものの)成功した時に2人が受け取る利得を55であるため,努力した方の利得は55-20=35であり,努力しなかった方の利得は55になる。よって,図1-10の利得表は以下のように書き換えられる。
近藤にとって,土方が「努力する」を選んだ場合には「努力する」の方が(60>55),土方が「努力しない」を選んだとしても「努力しない」の方が,利得が高い(35>30)。よって,近藤の支配戦略は,「努力する」である。土方も同様の理由から,支配戦は「努力する」である。以上から,両プレーヤーが支配戦略を選択すると考えられるため,予測される結果は(努力する,努力する)になる。この結果は,他のどの戦略の組み合わせよりも高い利得を両者に与えるため,パレート最適である。
チームで評価を行う場合,フリーライドを避ける最もシンプルな対策の一つが報酬額を高めることである。大成功の時にはとても高い報酬を,成功の時もそれなりに高い報酬を与えることで,「相手が努力しようがしまいが,努力して高い報酬をもらおう」というインセンティブを両者が抱くことになる。
問題1.2(強く支配される戦略の逐次消去)
(ア)
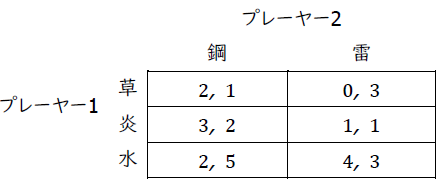
第1に,「草」は「炎」に支配されており,強く支配される戦略であるため消去する。第2に,「雷」は「鋼」に支配されており,強く支配される戦略であるため消去する。最後に,「水」は「炎」に支配されており,強く支配される戦略であるため消去する。よって,逐次消去の結果残った戦略の組み合わせは(炎,鋼)である。ちなみに私の知る限り,炎と鋼の2つのタイプを持つポケモンはヒードランのみである。
(イ)
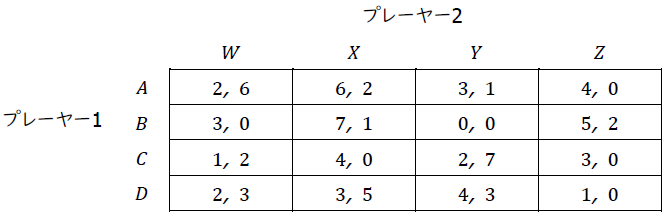
第1に,「C」は「A」に支配されており,強く支配される戦略であるため消去する。第2に,「Y」は「X」に支配されており,強く支配される戦略であるため消去する。第3に,「A」は「B」に支配されており,強く支配される戦略であるため消去する。第4に,「D」は「B」を支配されており,強く支配される戦略であるため消去する。(第3段階の時にすでに支配される戦略にはなっている。)第5に,「W」は「X」に支配されており,強く支配される戦略であるため消去する。(第4段階の時にすでに支配される戦略にはなっている。)第6に,「X」は「Z」に支配されており,強く支配される戦略であるため消去する。よって,逐次消去の結果残った戦略の組み合わせは(B,Z)である。
(ウ)
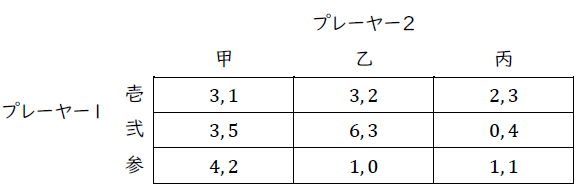
第1に,「乙」は「丙」に支配されており,強く支配される戦略であるため消去する。第2に,「弐」は「参」に支配されており,強く支配される戦略であるため消去する。これ以上消せるものはない。よって,逐次消去の結果残った戦略の組み合わせは(壱,甲),(壱,丙),(参,甲),および(参,丙)である。
(エ)
強く支配される戦略が存在せず,消去できるものはない。よって,すべての戦略の組み合わせが残る。ヒロアカで,誰と誰が今後対戦するかも,まだわからない。
問題1.3(サービス残業)
(ア) このゲームの利得表は以下の通りである。
(イ) 相手がサービス残業をしていた場合に,サービス残業を選択した方がより高い利得になる条件は,\(50-c>0\)であるので,\(c \lt 50\)であるので,同様に\(c \lt 50\)である。よって,「サービス残業をする」が支配戦略となる\(c\)の値は,\(c \lt 50\)である。
(ウ) (イ)とは逆の条件となるため,「サービス残業をしない」が支配戦略となる\(c\)の値は,\(c>50\)である。
(エ) 両者ともサービス残業をすることによって得られる利得\(50-c\)は,常に両者ともサービス残業をしない場合の利得\(50\)を下回っているため,パレート最適ではない。しかし,\(c \lt 50\)の時に,両者にとってサービス残業をすることが支配戦略となってしまい,両者ともサービス残業をすることが予測される結果になる。パレート最適ではない結果が生じてしまうという点で,「囚人のジレンマ」と同様の状況が生じてしまっている。
全員でサービス残業を拒否すれば,出世に響くこともなくサービス残業を避けることができる。しかし,他の人もサービス残業をやっている状況であれば,「上司に嫌われて出世に響くかもしれない」と恐れてしまうことで,誰も定時帰宅できなくなってしまう囚人のジレンマ状態に陥ってしまう。ちなみに,この簡単な解決策が,上司がサービス残業を強要せずに,定時帰宅を推奨することであることは言うまでもない。