出世で給料が上がる理由

PDFファイル

【森谷文利】

1. 出世と給料

第７章では戦争を題材にして，ベイズ・ルールを学習しました。講和に応じるのは自国が劣位である可能性が高まったからだ。そう議論したわけです。このように追加情報の観点から，現実を理解するのは国際政治学だけではありません。話題を大きく変えて，企業で働く従業員の昇進について考えてみましょう。

給料は多いにこしたことはありませんが，「給料を増やすために昇進をしたいですか」と聞かれると躊躇する人は多くいると思います。以下の事例を通して，昇進と賃金の関係を考えてみましょう。

昇進が給料を増やす理由を生産性の側面から理解する人は多くいます。「会社の利益を左右する立場にあるから」とか，「責任が増えるから」といった理解です。しかし，給料が増える理由はそれだけでありません。出世には，ポストにふさわしい人を配置する必要がありますが，企業は，誰がその仕事に適任かを最初は知りません。この不確実性が原因となり，給料を高めることもあります。本オンライン・コンテンツでは，不確実性があると出世によって給料が増える理由をWaldman(1984)にもとづいて考えてみましょう。

2. 学習プロセスからみた昇進

従業員の昇進に関するモデルを次のように設定してみましょう。昇進によって給料の引き上げが必要な理由を明確にするため，以下のモデルではあえて昇進によっても給料が変わらないようにしています。

プロジェクトに成功したとき，ワルオさんを昇進させるべきだろうか？ ただし，昇進にかかわらず，ワルオさんの年収は変わらないとする。

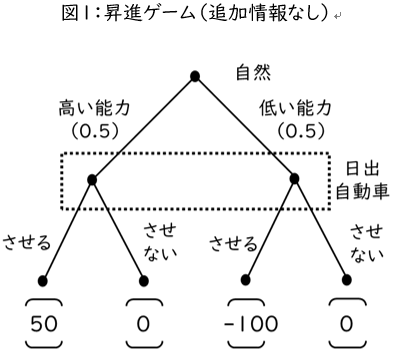
本モデルではワルオさんの能力がわからない状況を取り扱っています。プロジェクトを任す前の状況をゲームの木で書くと図1のようになります。最初に自然がワルオさんの能力を定め，次に日出自動車がワルオさんを昇進させるかどうかを決めます。ここで日出自動車の意思決定点が情報集合で囲まれていることに注意してください。ワルオさんの能力を日出自動車は知らないからです。

このようにこのモデルでは能力に関して不確実性があります。このような場合には，期待利得を計算して議論するのでした。能力が高い確率を\(\textrm{P(高い)}\)と表現すると，\(\textrm{P(高い)＝P(低い)＝0.5}\)ですので，

\[\begin{align}
& \textrm{(「昇進させる」の利得) }\\
&=0.5×(100-50)+0.5×(-50-50) \\
&=-25<0 =\textrm{(「昇進させない」の利得)} \\
\end{align}\]

となります。したがって，プロジェクトを任せる前は，昇進させないことが良いことになります。

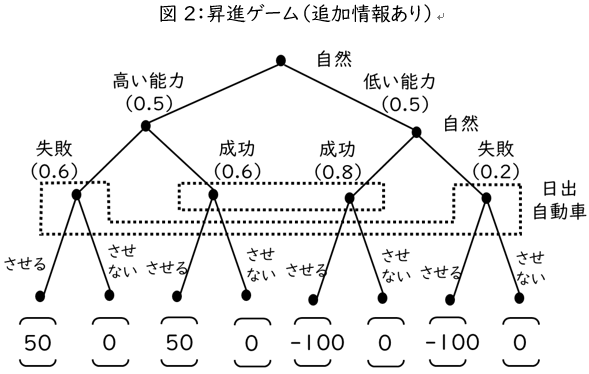
では，プロジェクトを任せて成功した後はどうでしょうか。プロジェクトの結果という追加情報が得られるので，ゲームの木は図2のようになります。モデルで説明した「成功確率」は条件付確率であることに注意してください。高い能力であるときの成功確率は，「能力が高いことを条件とした成功の確率」だからです。

成功を観察した後を考えましょう。ここで知りたいのは，成功したワルオさんの能力が高い確率です。つまり，\(\textrm{P(高い∣成功)}\)です。ベイズ・ルールによって

\[\begin{align}
&\textrm{P(高い∣成功)}=\frac{\textrm{P(成功∣高い)}}{\textrm{P(成功)}}\textrm{P(高い)} \\
&=\frac{0.6}{(0.5×0.6+0.5×0.2)×0.5} \\
&=\frac{3}{4}
\end{align}\]

となります。ワルオさんが高い能力の可能性は\(0.5\)でしたから，成功という追加情報を得ることで まで高くなっています。したがって，期待利得を計算すると，

\[\begin{align}
&\textrm{（「昇進させる」の利得）}=\frac{3}{4}×50+\frac{1}{4}×(-100) \\
&=12.5>0=\textrm{(「昇進させない」の利得)} \\
\end{align}\]

となりますので，昇進させることが得になっています。プロジェクトに成功した後，企業はワルオさんを昇進させるようになります。逆に，失敗すると，能力が高い確率は\(1/3\)まで低下しますので，期待利得は

\[\begin{align}
&\textrm{(「昇進させる」の利得)}=\frac{1}{3}×50+\frac{2}{3}×(-100) \\
&=\frac{-150}{3}<0=\textrm{(「昇進させない」の利得)} \\
\end{align}\]

となり，昇進させません。このように「会社で働く」というのは，労働力の対価として賃金を支払うという関係だけではなく，従業員の適性を発見するプロセスとしての側面もあります。こうした学習プロセスの結果，昇進させるかどうかを決めることになります。

3. シグナリングと引き抜き

学習プロセスの結果として昇進を理解すると，昇進によって給料が上がるもう一つの理由が浮き彫りになります。昇進したということは能力が高いと日出自動車が判断したということですから，そのことが他社に伝わると，ワルオさんが引き抜かれる恐れが生じるからです。実際にライバル社の斜陽自動車が登場するモデル2を考えてみましょう。

新しいニュースが飛び込む前の状況から考えましょう。この場合，能力が高い確率と低い確率は半々だと思っているので，支払える上限は，期待値をとって

\[0.5×80+0.5×10=45万円\]

となります。ワルオさんのもともとの給料は50万円でしたから，斜陽自動車は引き抜きがうまくいきません。

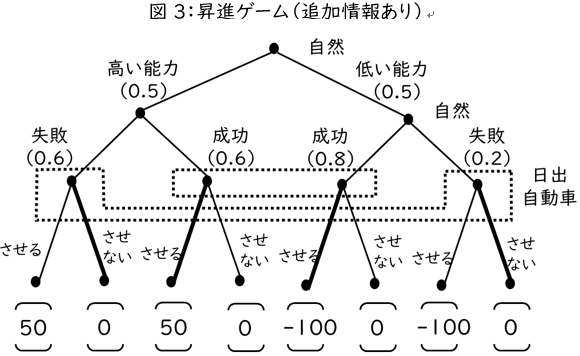
しかし，出世したワルオさんなら話は別です。図3を見てください。先ほどのモデル1で計算した日出自動車の最適行動を太線で表しています。この図をみるとプロジェクトが成功したときのみ，昇進させています。したがって，プロジェクトの成否をしらなかったとしても，斜陽自動車は，「昇進の有無」で推測することができます。出世した場合にはプロジェクトに成功しているということですから，先ほどと同様にベイズ・ルールに基づいて，能力が高い確率を

\[\begin{align}
& \textrm{P(高い∣成功)}=\frac{\textrm{P(成功∣高い)}}{\textrm{P(成功)}} \textrm{P(高い)}\\
& =\frac{0.6}{(0.5×0.6+0.5×0.2)×0.5}=\frac{3}{4}\\
\end{align}\]

と計算できます。この確率に基づいて，斜陽自動車がワルオさんに提示できる上限を計算すると，

\[\frac{3}{4}×80+\frac{1}{4}×10=62.5万円\]

となります。出世したワルオさんは高い能力である可能性が高まりますから，斜陽自動車は高い給料を支払えるより，ワルオさんの現在の給料50万円を上回る提案ができます。逆に，日出自動車からすると，今の50万円の給料を維持していると，斜陽自動車に引き抜かれてしまいますから，給料を上げる必要性が出てきます。これが昇進によって給料が上がる理由です。ある従業員の昇進は，「他の会社に対してその従業員の能力が高い」ということを伝えてしまいます。そうなると，ライバルからの引き抜きの脅威に直面するので，給料を上げるようになるということになるわけです（シグナリング仮説）。

シグナリング仮説の重要な前提は斜陽自動車と日出自動車の間に情報の非対称性があるということです。引き抜こうとする斜陽自動車からすると，日出自動車でのワルオさんの働きぶりを知ることはできません。他方，ワルオさんが現に働いている日出自動車はその情報を知っています。それゆえに，ワルオさんを出世させると，「日出自動車が出世させたのだから，きっと能力が高いにちがいない」と推測し，ワルオさんの（期待値での）能力を上方修正しているわけです。

ここまでワルオさんの話でしたが，現実に目を向けても，シグナリング仮説は妥当なものだと考えられます。現実のデータからわかることを上手く説明できているからです。例えば，労働者の質の影響を取り除いたとしても，大企業は中小企業よりも平均的に35％高い給料を従業員に支払っています(Brown, Hamilton and Medoff, 1990)。また，こうした大企業と中小企業の給与の違いはより高い地位に出世するほど大きくなります(Brown and Medoff, 1989)。こうした事実は，生産性の観点からすると不思議に見えるかもしれません。同じような仕事をしているのに大きな給与格差があるからです。しかし，シグナリング仮説を考えると自然です。大企業の方が出世するには高い能力が求められますし，その能力は地位が上がるほど大きくなるでしょうから，非常に高い能力だということが他社に伝わり，より高い給与で引き抜かれる可能性が大きくなります。結果，こうした給与の違いが表れてくると考えられるのです(Zabojnik and Bernhardt, 2001）。

さて，出世を嫌がる風潮に話を戻しましょう。本コンテンツの冒頭では，出世を嫌がる理由として「わりに合わない」と考える人が多いことを紹介しました。特に給料と仕事内容が見合わないという意見がありました。しかし，シグナリング仮説が正しいならば，転職などの将来のキャリア形成からメリットをとらえなおす必要があります。苦労が現在の給料と見合わなかったとしても，出世することは皆さんの能力が高いことの証明であり，転職市場で有利だからです。現在の給料と将来の転職による給与の増加の両方のメリットを考える必要があるように思います。とはいえ，こうした議論は転職しやすいことが前提条件です。日本の労働市場では転職しにくいといわれていますので，シグナリング仮説を原因とした給料の上昇はあまり大きなものではないのかもしれません。もしそうだとすると，現在と将来の給料を合わせても，本当に出世は見合わないものかれません。

本コンテンツでは，出世についてシグナリング仮説を中心に紹介しましたが，生産性やシグナリング仮説以外にも仮説は存在します。トーナメント仮説など理論の全体は，Waldman(2013)を参照してください。

参考文献

• 荻島央江（2022）「昭和世代は驚愕！？ 若者の83％が『出世は勘弁』」日経ビジネス2022年11月7日（2023年２月6日参照）
• Brown, Charles, Hamilton, James and James Medoff (1990) Employers Large and Small, Cambridge: Harvard University Press.
• Brown, Charles, and James Medoff (1989) “The Employer Size-Wage Effect,” Journal of Political Economy, vol.7, no.5, pp.1027–59. JSTOR.
• Waldman, Michael (1984) “Job Assignments, Signalling, and Efficiency,” The RAND Journal of Economics, vol. 15, no. 2, pp. 255–67. JSTOR
• Waldman, Michael (2013) “Theory and Evidence in Internal Labor Markets,” in Handbook of Organizational Economics, edited by: Robert Gibbons and John Roberts, Princeton University Press, pp. 520-571.
• Zábojník, Ján, and Dan Bernhardt (2001) “Corporate Tournaments, Human Capital Acquisition, and the Firm Size-Wage Relation,” The Review of Economic Studies, vol. 68, no. 3, pp. 693–716. JSTOR.